关于不完备性定理和不确定性原理的探讨 (小结) * K5 s6 [" X5 |) O: B
p, W( N4 A: ~9 C( j3 Q: y2 I( B G, p% m' d
) V0 [" ?' `0 J
一、不完备性定理简述9 s6 N2 A: K$ p) G* D" h2 o
1931年哥德尔发表论文《论数学原理和有关系统的形式不可判定命题》,即著名的哥德尔不完备性定理,其核心脉络大致可以分为这样三个步骤: (步骤一:数字化同构)不完备性定理证明方法的奇思妙想是把自然语言数字化,哥德尔在文中大量篇幅花费在十分繁琐的映射定义上,以便把自然语言映射为数字。因为自然语言可以转换为形式逻辑、形式逻辑可以演算成命题范式、而命题范式可以展开成为标准的逻辑门、并且逻辑门可视作一种二进制代码。比如逻辑门“与”可对应为01,逻辑门“或”可对应为10,逻辑门“非”可对应为11。然后二进制数再转换成小数,如0.1,0.01,0.11,因此形式逻辑运算不过是这三种码的组合。所以即使非常复杂的逻辑门组合,也只是小数点后的尾巴更长点而已,仍然还是个小数。也就是说‘自然语言系统’通过转换为命题逻辑门,恰巧可以对应于一个‘算术公理系统’的小数(有理数)。 哥德尔通过一种十分新颖的同构映射形式,把‘自然语言系统’和‘算术公理系统’联系到了一起。然后,对于原本并不严谨的自然语言的语义的证明,也就变成了惯常熟知的相对简单的严格算术证明。哥德尔天才的洞察力,发现了‘自然语言系统’和‘算术公理系统’的映射同构关系,这是解决自然语言系统语义歧义的关键。
G# I6 ~5 W) d ~1 c% V4 W: K
(步骤二:代数数与超越数的区别)历史上,有一些悖论,比如理发师悖论提出后,数学家们发现可以通过对集合论进行改造、通过对集合补充定义来排除悖论。当一个形式逻辑体系出现上述悖论时,就用一个更大的逻辑体系去包络它,让原先那个逻辑体系作为更大的逻辑体系的子集合。当然这样做的结果,新的母体系又可能产生新的矛盾。但这也没关系,只要类似地一层一层地包下去,逻辑系统空间从n维扩充为n+1维,以致于无穷维。依此类推,似乎所有的问题命题总能通过递归嵌套,从而针对性化解。希尔伯特、罗素等数学家都坚信,任何数学真理,只要通过一代又一代人的不断努力,都能依靠不断扩张的n+1维公理的逻辑系统化将其整合到数学的大厦中。简单来看,把一个有歧义的命题分而析之各个击破,相当于细化切分问题。类似于“一尺之捶,日取其半,万世不竭。”我们知道,以这种一刀一刀砍出来小段,其实就是一个分数(有理数)的数列。哥德尔把这种可以通过层层外延扩张的n+1维公理系统称为递归集。 但是,哥德尔发现,还存在另外一些逻辑悖论,比如说谎者诡论,相当于“非递归集”,并不能通过递归集得到完整表达。这类似于“超越数”,它超出了整个代数系统解答能力,超越数对代数系统而言,是不可判定命题。
) n3 n, A" E3 W! X" I
(步骤三:阿列夫0对阿列夫1的不完备)超越数是无理数的主力军,也是稠密实数的主要组成部分。康托尔证明了‘不可列’超越数比‘可列’有理数要多得多[2]。可列集合的势为阿列夫0,不可列集合的势为阿列夫1 。类似于阿列夫1之多的超越数对于阿列夫0维度的代数系统不可判定,哥德尔印证了不可列的“非递归集”对于可列的的形式逻辑系统是不可判定的。 可见,不完备性定理的本质是空间维度的不完备。 : F- w+ g! g3 j, G' Q) X! a
; a i% o- v) U
; u. a' S6 a' z9 T. q! X
' @$ o) ?0 j7 ^
. ?/ p5 Z8 A9 _" v2 g! C
二、不确定性原理与维度不完备 著名的‘波爱之争’中,波尔坚信矩阵力学是完备的,因为其依赖的希尔伯特空间具备柯西序列内部收敛性,普遍观点认为这意味着数学上的完备性。 但爱因斯坦却坚持认为量子力学是不完备的。依直觉而言这似乎是显然的,因为参照系的不完备将导致数据记录的不完备,因而出现不确定性。维度不完备往往是不确定性现象产生的根源。这就像六个面的骰子,如果我们在骰子的每一个面都有一台摄像机记录,那么对骰子的记录是全面完整确定的;只有当骰子投掷只显示一个面情况时,记录是概率性的。 量子力学到底是不是完备的理论体系,在‘波爱之争’之后也一直未有定论。本文尝试对这一问题作进一步探讨。
% W# `7 o+ O( s+ [下面,先来看一个具体直观的例子:泡利矩阵

8 {/ }2 K* M, l' k& c3 V$ k0 v
5 m1 k0 z. P4 X. K9 ~ 众所周知,σx矩阵和σy矩阵不对易,说明其共同本征函数系不完备。那么也许需要先弄清楚,其完备的共同本征函数系是几维的?表面上看二维的泡利矩阵当然是二维的。但是,泡利矩阵的二维并不是一个维度取自于实体空间x轴,另一个维度取自于y轴,而是取自复数空间的某个正、负的方向,而这方向同时和x、y、z三维相关。所以自旋空间有且只有三个泡利矩阵,而不会是两个或四个泡利矩阵。所以σx乘以σy并不是二维空间,而是个三维空间的,所以众所周知的,泡利矩阵σx、σy、σz互相不对易。其不对易的根源在于彼此没有共同的完备的基矢量。也就是说,σx、σy、σz的共同基矢量只有正负方向的二维,但是却需要表达一个三维空间。这不正是“不完备性定理”的本质问题么?(因为基矢量对空间维度不足够,所以表达不完备)3 ]( u) Z R- u# p, _6 U
有限维度的矩阵的不完备性容易理解。不过我们知道哥本哈根矩阵力学的‘矩阵’是基于微积分表述的连续无限维度的,莫非连续无限维的基矢量也不完备么?
( c, N/ N$ ~( K. C0 [3 M3 D: X5 F( |
为此,我们来探讨一个不确定性原理的特例——高斯函数。高斯函数应用范围很广,在自然科学、社会科学、数学以及工程学等领域都能看到它的身影。高斯函数是不确定性原理的最简单、最典型、最清晰、最有说服力的例子。 【命题】矩阵力学的高斯函数的exp(ikx)本征函数系不完备 : l* v$ k; _- W6 I) h. l
【证明: (步骤一:高斯函数原函数与其傅里叶变换函数,存在不确定性关系) 
J1 K: g0 G0 F+ L! }' ~% p
' P/ ^9 ?) m; `: ?- p. C$ x
8 E6 l# E5 g$ n4 ?9 o9 \! D
0 Q+ \' W' V/ S; E
: O4 E) j: p0 U. C6 |+ |
; F3 A* x9 I h4 j
: Q" p) G1 R7 i$ t! }5 h% K* G' }
e1 p2 O4 D- W7 V
7 b6 ]6 ^, t; j9 G* H4 r, O
―――――――――――――――――――――――――――――――――――――
3 E1 V2 x: d5 j, Q [注1:这是基于连续无穷维矩阵的表达式。
' {1 q) i1 M- ~1 S8 O' n8 P( {
$ @" k3 V: B" H; a4 m+ ^
- _( d5 w4 p+ F
(步骤二:高斯函数原函数与其傅里叶变换函数,存在一组共同本征函数exp(ikx) ) * ~8 w' z( _1 J, T8 T
先证明高斯函数的傅立叶变换后还是高斯函数: 
9 x; Q) H! y. s( Y5 u; t3 w
证明了高斯函数的傅立叶变换后还是高斯函数,其实也就间接说明了高斯函数之间具备共同本证函数。 设高斯函数傅立叶变换函数为φ(k),高斯函数原函数为ψ(x),有: 
7 X" _3 R3 |8 p+ N/ X7 ~+ P4 t0 p+ B
知:exp(ikx)是高斯函数傅立叶变换函数φ(k)的本证函数 又,由于高斯函数的傅立叶变换后还是高斯函数,可知exp(ikx)也是高斯函数原函数ψ(x)的本证函数。 很显然,exp(ikx)既是高斯波包原函数的本证函数、同时也是高斯函数傅立叶变换函数的本证函数。事实上,高斯函数原函数和高斯函数傅立叶变换函数,其实都是高斯函数。也就是说,高斯函数本身就是傅立叶变换的特征函数。既然不同高斯函数之间区别仅仅是系数不一样,它们当然具有共同的本证函数。当然也就不奇怪exp(ikx)是其中一个的本证函数,也就肯定是另一个的本证函数。 9 V. \0 y, L5 W3 u3 p2 W7 l
9 d6 K% [0 D. L' Z$ o3 N& J7 @
' t9 L: m! l" j8 p3 G
(步骤三:高斯函数与其傅里叶变换函数的以exp(ikx)为基的共同空间不完备) 反证:如果矩阵表达的高斯函数和其傅立叶变换函数的以exp(ikx)为基共同空间是完备空间,由对易算符定律:  , l8 \* b" K1 N) s7 |) {; t1 ^+ s , l8 \* b" K1 N) s7 |) {; t1 ^+ s
则推导出,存在一组完备的共同本征函数系exp(ikx),使高斯函数和其傅立叶变换函数的矩阵表达式对易,这与上面‘步骤一’关于这两个函数存在不确定度关系的结论矛盾。 所以,矩阵表达的高斯函数和其傅立叶变换函数的共同本征函数exp(ikx)不完备 ――――――――――――――――――――――――――――――――――――――― [注2:exp(ikx),常常也记作exp(ipx)、exp(ipr)、exp(ipq)、exp(iEt)、exp(ist)等等。即自然数e的ipx次方,其中i是复数符号、p和x分别是傅立叶变换中的函数变量。
" E; \- [9 t5 N5 `; G/ J9 i9 S0 s2 u
7 y- j9 I, }: a. o7 @
证明简洁、无懈可击。 高斯函数的exp(ikx)本征函数系居然是不完备的,很令人费解。 其根源在于向量空间(平面矩阵)的局限性。因为完备的exp(ikx)本征函数系超出了平面矩阵乘载范围,完备的exp(ikx)本征函数系是一个高阶张量空间。下面以单个电子的夫琅禾费点孔衍射实验来形象说明。 4 p5 z3 S. q4 }+ }
/ \$ o' y- U: r$ M5 I
1 z, [2 h z u4 H# N' ^' z
0 m( n/ _( O* B4 k( [+ l% t
z& Q# C2 i2 i' k; R. ]
; t, D% e" x4 {* p; l
' a% R5 [- r* E
' Y* y- g, Z# v- ]/ D" y9 m
: x6 v2 G! b, L; d8 M
. P* d; Z' @ Y0 O, r% I
- }' [8 N: J- d7 F1 _8 k4 K
三、单电子夫琅禾费点孔衍射实验 阿列夫2维度空间对于大多数人而言可能比较陌生。下面,以“单个电子的夫琅禾费点孔衍射图”来分析,我们能够从中更深入了解阿列夫2维度与量子态空间的内涵、了解不确定性原理与维度不完备的关系。 众所周知,通常的夫琅禾费衍射是“一束”平行光(或一束电子)通过一个方形小孔,形成sinc函数的衍射图形。这个实验形象地定格了量子在频域和空域的波粒二象性的现象,和理论完全一致。一头是‘矩形’小孔、另一头是‘sinc’衍射,而‘矩形’图的傅立叶变换正好是‘sinc’函数图象。因为直观简洁,这个实验常常用来解释不确定性原理。 一束电子的衍射大家都非常熟悉。但是单个电子穿过夫琅禾费实验的点孔的衍射图会是个什么样子呢?答案可能会让人很意外。 
+ j% P& v4 _& q
我们可以大致推断单电子夫琅禾费点孔实验,最有可能出现以下三者情况: 1、接受屏上出现一个均匀分布的光板 
* ^! V9 N5 k' X
我们知道一束白光的夫琅禾费单孔衍射图样中各色光排列为‘中间白色,然后依次向外为: 紫、 靛、 蓝 、绿、 黄、 橙、 红 ’。可以看出,光的波长越短,缝相对而言就越宽,孔径越宽,衍射现象越窄缩,则光强变强、条纹变窄;另一方面,波长越长,缝相对而言就越窄,孔径越窄,衍射现象越宽阔,则光强变弱、宽度变宽。光子波长相对较长,衍射现象条纹会将对较宽,以至当孔逢过小时,光影会扩散为整个屏,形成一个均匀分布的光板。冲击函数δ的傅里叶变换清楚表明了这个现象的理论基础。继而,根据光子的波色凝聚效应可以推断,一束光的每一个光子都是同态的,也就是说一个单光子的结果和一束光是一样的,所以说当单个光子通过夫琅禾费微孔后,接受屏上会出现一个均匀分布的光板。 既然单光子通过夫琅禾费微孔会出现一个均匀分布的光板,那么单电子通过夫琅禾费点孔接受屏也会出现同样的光板吗?答案是不会。 因为电子是费米子,不具备波色凝聚效应。根据泡利不相容原理,各电子之间不可能完全同态,因此一个电子的衍射和一束电子的衍射图不可能完全一样。即使一束电子在接受屏能够产生均匀分布的光板(这也值得怀疑),那也不是n个电子的一模一样的衍射图案(均匀分布光板)叠加出来的。另一方面,如果一个电子产生了均匀分布的衍射光板,根据泡利不相容原理,各电子之间不可能完全同态,第二个电子就不能再产生均匀分布的光板,则第一个电子和第二个电子的傅立叶变换图像出现差异。即第一个电子满足δ冲激函数的傅立叶变换时,第二个电子不满足。这显然不可能。 因此单电子夫琅禾费点孔实验接受屏上不会出现一个均匀分布的光板。 2、接受屏上是一个sinc衍射图形:  4 g* G: n/ s, V+ N 4 g* G: n/ s, V+ N
这是大家熟知的一束电子通过一个方形小孔的夫琅禾费衍射图象,实验和理论高度吻合,因此很多参考文章以夫琅禾费sinc衍射图形来解释不确定原理: 
4 `9 U) @( r5 k$ j/ g p! z1 R% Z' I" J) e e, O
证明过程简洁清晰,不过非常遗憾,上面这个关于夫琅禾费衍射和不确定性原理的证明解释是有问题的。请看下面分析:  + F+ `! Z, Y- S( ?) K4 g: u + F+ `! Z, Y- S( ?) K4 g: u
但是: 
8 _* Q4 s' S0 d/ v
很明显,上述的(2)和(1)矛盾。 上面推论过程的谬误根源在于隐含假设了电子波是“实体波”。但这是不可能的,因为实体物质波包必然会扩散。而如果电子是膨胀扩散的波包,这当然与事实(电子总是固定大小的)不符。下面是关于‘实体物质波’不可能存在的证明:
4 n: j" n& w7 G2 e
, N9 Y$ |) @( Y9 v% f 因此单电子夫琅禾费点孔实验接受屏上不会出现一个sinc衍射图形。
) S& P0 C# p1 z
& o+ t2 c6 w) |5 h; N1 ?0 a3 P
1 C3 }; `1 w0 Z/ b/ i7 m
9 F( [& w/ x- f6 l8 d3、接受屏上出现一个点: 
既然单个电子通过夫琅禾费点孔,接受屏上不可能出现一个均匀分布的光板、不可能出现sinc函数图形的衍射,那么似乎可以判断接受屏上应该出现一个点。乍看之下,这样思考当然是有一定道理的,我们知道电子波长相对很短,即使其有衍射现象条纹当然也会非常窄,以至于缩小为一个点。无数次电子衍射实验表明电子总是一个点一个点到达屏上,然后这些点电子根据泡利不相容原理(费米子不能处于同一个状态),电子靶点各不相同,大量电子点共同汇集成了衍射图像。 但是,当我们进一步分析时会发现其中的谬误:因为夫琅禾费装置的两端对应于傅立叶变换的两对偶域,比如障碍屏和接受屏分别对应于频域和时域,所以障碍屏和接受屏不可能同时是“点”,否则违反不确定性原理。 
6 E5 T. _, N/ f& H
傅立叶变换运算规则告诉我们,在实体空间中<q|X> 和<p|X>不可能同时是确定的"点”值。如果当障碍屏小孔等效为等式左边的波函数<q|X>时,这时<q|X>看作是“粒子”态(非零值投影到X>的区域有限),则等式右边的<p|X>必然是无穷无尽的频率“波”(非零值投影到X>的区域无限)。 这意味着,当我们在接受屏看到一个电子点时,则夫琅禾费障碍频的孔应该很宽,不可能是一个“点”孔。另一方面,如果夫琅禾费小孔充分狭窄至“点”孔,则接受屏不应该出现一个电子“点”。任何物理量在频域和时域取值范围都不能同时有限,这就是著名的“不确定性原理”。 因此,单电子夫琅禾费“点”孔实验接受屏上不能出现一个“点”图形。
+ s: D) a- _1 }7 [+ s/ z
那么,既然上面的三种情况的推演都会出现谬误,单电子夫琅禾费点孔实验到底会发生情况呢? - ~. z0 M' R9 A3 q* R: @
% n+ z, J u* X( O' F% j
7 @ V, d _5 q
6 d0 V0 V a, A* C" I! ?
9 l2 l# i. g/ W3 |
" h0 {( f* n# v5 }% h
9 k( E2 s7 l- P9 B7 P. C) Q+ Q% J# r3 x
7 _# U* A9 z- {: {
/ v& i) b r. ?/ q) d6 d
四、粒子实体坐标{x}和位置算符的本征态x的区别 上述的夫琅禾费衍射分析之所以进入死胡同,究其根本是因为其逻辑推演过程拘泥于粒子实体空间,困扰于经典物理的狭隘思维。对经典物理粒子的实体空间的线性表达在数学形式上与平面矩阵是等价的,而平面矩阵却存在局限性。如下图,如果假定中间的exp(ipr)矩阵是傅立叶级数的展开式,则“单电子”和“点孔”概念等效于矩阵式中的ψ(r2)和φ(p2)两个元素点 。但如果仅仅ψ(r2)和φ(p2)两个点有非零值,则意味着中间的矩阵并不是傅立叶变换,因为这违反不确定性原理。而真正的傅立叶变换与不确定性原理是自洽一致的。 
' c/ s* e$ m! R+ l6 |
进一步分析,由于傅立叶变换中的对偶域空间模型,实际对应的是张量的概念。所以如果我们把有局限性的平面矩阵扩展为高阶张量时,是可以有效化解上述逻辑谬误的。如下图: 
/ X2 v. D ]4 m$ Z
# c) c: x' g9 e' Q9 [
3 b7 a! Q( D, m* ^; ?4 l! o* `在上面的高阶张量演算式中,把原来的平面矩阵的一个元素φ(p2)扩张成了张量中的一列3元素φ(p21)、φ(p22)......φ(p2n)等。需要特别指出的是,这里的φ(p21)、φ(p22)......φ(p2n)既不是实体小孔的数值、也不是实体投影点的数值,它们不是任何实体的夫琅禾费实验的演示设备或图形的实体坐标值,而是单个电子“穿过”障碍孔的逻辑概率。很早物理学家们就注意到量子现象与经典物理现象有本质不同。在经典物理中,一个物体绝对不可能穿过比它自身更小的障碍孔,当障碍屏“点孔”非常小时,经典粒子将会比“点孔”大,这时经典粒子不能通过比其更小的“点孔”。但是对于量子现象则有所不同,类似贯穿势垒的量子隧穿效应,具备某能量(频率)电子将会闯过障碍“点孔”、另一些则穿不过去。这对于单个电子而言,相当于逻辑上的概率性,而这种表征不同频率(可能还包含自旋方向、角动量等等不同属性)的电子的穿透性的概率幅,表征了‘概率本证态’。
――――――――――――――――――――――――――――――― [注3:为方便表述,可连续取值的张量空间这里以离散值简化
# K$ |5 F* |7 h% v
2 ]& N& e$ C- f% B3 Y, R' D
$ j8 d; F9 O, E* }* \
5 |( |- e0 h3 X- ?* e+ ]" u. o) ^
! _" \/ {0 D! f: k
; j0 k- B9 O2 F4 m, \( ?
值得庆幸的是,在高阶张量模型中,可以对单电子夫琅禾费点孔实验的 “单电子”、“点孔”和量子隧穿效应的“概率幅”等要素一一对应、完整表达。相应地,经典物理实体动量{p}由一个点值扩张成了一系列概率本证值p21、p22.....p2n等。需要注意的是,这种概率本证态的概率幅相当于动量算符的本征值p,而不是实体动量{p}。4 而这正是问题的关键,如果我们仔细审视,会发现上文关于单电子夫琅禾费点孔实验的分析中,混淆了粒子实体坐标{x}和位置算符的本征值x 的概念。在量子力学中,实体坐标和算符本征值是完全不同的两个概念。上一节的探讨中,所谓的“单电子”和“点孔”的概念都是经典物理的实体坐标的概念。但在量子力学中,量子态的意义要广泛得多,不仅仅局限于实体坐标,还包含了‘概率本证态’等新要素。 比如我们知道,不确定性关系△x△p=h/2 中的x和p并非粒子的实体坐标{x}和实体动量{p}概念,而是粒子的位置算符和动量算符的本征值的概率化反映。 / O) b/ r1 ~! s) N/ ^4 T" `
借此,让我们再回过头审视波爱之争的焦点。为什么波尔和爱因斯坦为此争论数十年无果,为什么很多物理学家乐此不疲议论了一整个世纪还在争论不休?根源亦在于此,因为他们混淆了坐标实际位置和位置算符本征值的概念。表面上粒子实体坐标{x}和位置算符的本征值x 好像都代表‘位置’的概念,但此位置不是彼位置。爱因斯坦观念中的粒子实体坐标{x}是基于经典力学机械决定论度量的,而机械决定论只讨论实体点坐标,所以{x}只能是实数连续(阿列夫1维度)空间的概念。而波尔观念中的位置算符的本征值x所处的态空间是阿列夫2维度的,本征值x实际上是阿列夫2维度的投影。它是阿列夫2维度空间的概念,所以它在实体坐标中体现为概率值。显而易见,位置算符本征值x和经典物理的实体坐标{x}根本不是一回事。粒子实体坐标{x}和位置算符的本征值x有本质区别。也就是说,表面上爱因斯坦和波尔虽然都在谈位置变量,但是他们谈的并不是同一回事。它们两者一个是阿列夫1维度的概念、一个是阿列夫2维度的概念。 + I! C2 ?& P. s2 W& W( {& h
需要特别指出的是,不同维度下对应于不同意义的概念,这也许并不那么醒目。但是在逻辑分析时概念维度却不容忽视。假如维度不一致,即使相同名字的概念也并不等价。比如,有一个这样的所谓的高级数学题: " K/ ]" P2 J, q7 Z7 s7 V
【求证:1元=1分
( n3 t& I+ r- C2 Q/ k解:
1元=100分 =10分×10分 =1角 ×1角 =0.1元×0.1元 =0.01元 =1分
/ E2 X9 K% H2 O0 I9 m4 f】
上面的逻辑谬误就是一个典型的概念混淆,其关键点是‘100分’和‘10分×10分’相等吗? 相信大多数读者都知道,100分和10分×10分不相等。究其根本,因为其中的‘分’和‘分×分’是完全不同的概念。‘分’是一维概念,‘分×分’是二维概念。一维变元和二维变元,在逻辑上有本质区别,根本不可能划等号。如果强行划等号,逻辑谬误在所难免。 " a7 N, F# R! R. M& `3 a* V
――――――――――――――――――――――――――――――― [注4:为简化描述,本段的本征值p和x未予以区分。
% [- |8 `! d% D
: H+ m4 Y5 B4 q2 w/ u1 k- r9 P, X; z
% z8 b4 e! [; |; i4 G/ U
* r x% ~5 P2 K$ f) v/ s [( y3 b
, T) Q& V- b* Y. w2 i
+ F4 r: h$ P. x' v& y- g0 F9 ]
3 A" b, ]* F) Z3 L6 A
粒子实体坐标{x}和位置算符的本征值x的区别,还可以从δ(x-p)的傅里叶变换演算中看出来。如果我们对{x}和x不加区别,就会出现如下谬误: 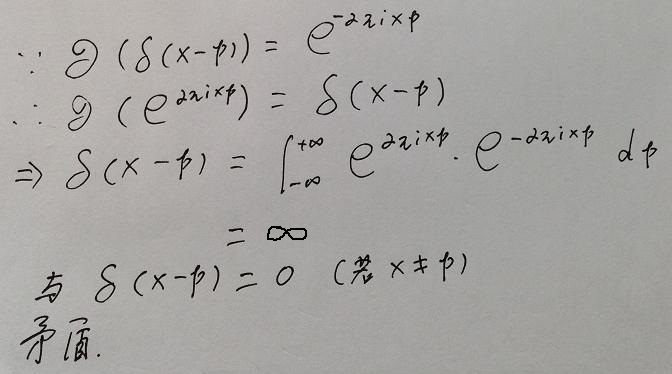 ) z: m% R$ L) A# n( u4 x& N ) z: m% R$ L) A# n( u4 x& N
如果我们有效的区分了{p}和p,则exp(ipx):的正交性就一目了然:  9 s @1 K+ S" j( u- a( r6 B 9 s @1 K+ S" j( u- a( r6 B
( Y9 ^( l! c& T) |
1 Y. x9 |5 p) n+ Q* _3 R; H5 f
; o" W4 U! v" T- b0 p―――――――――――――――――――――――――――――――
[注5:动量p可以表达为(-id/dx),即p可看作x的函数。 ! L% j$ |- f% u$ _3 k5 R0 Z+ I
# {' Z/ e; Y0 y* `+ r r
" e+ m0 i# g- P( d( i
, ], i1 P) A' \- F6 m" E7 F
; e# }, w) E% k s: T z- g
8 Z6 j1 S/ N3 F9 x- \3 j8 A# k, F3 s
五、连续无穷维平面矩阵的不完备性 上一节,我们发现单电子夫琅禾费点孔实验推断三种结果之所以产生狭隘解释,追根溯源是因为平面矩阵下思维的狭隘性。那么,如果我们把平面矩阵扩充到无穷维,甚至连续无穷维,能不能解决类似的局限性问题呢?我们知道,连续无穷维矩阵,正是哥本哈根矩阵力学的根基。 深入探讨连续无穷维矩阵问题之前,需要我们再回头进一步审视高斯函数。第三节提到exp(ipx) 是高斯函数的本证函数,乍看之下这种提法一时难以让人接受。因为教科书中,一直把高斯波包ψ(r)本身和其傅立叶变换函数φ(p)看作波函数(量子态)。似乎没有人提出过平面波函数exp(ipx) 亦可以看作量子态。  1 @8 v& s8 O% w 1 @8 v& s8 O% w
但是,另一方面,我们知道在傅立叶分解时,其实是把exp(ipx) 作为基矢量,而把原函数ψ(r)看作其傅立叶变换函数φ(p)的投影值。如果把exp(ipx) 作为基矢量,当然也就意味着exp(ipx) 是φ(p)的本证态。
" h& F- B5 _- D ?: m# z再回头看看傅立叶变换的矩阵表达式:

" d: S4 f8 O, [' ?3 @
1807年,法国数学家傅立叶向巴黎科学院递交了一篇论文《固体中的热传播》,在这篇研究热传导问题论文里的有一个当初并不起眼的副产品:任何一个信号(或者说一个函数)都可以表达为一系列不同频率的简谐振动(即平面波)的叠加。 把函数分解到简谐振动(即平面波)的叠加,即以exp(ipx) 基底 。
( |& S: G) j# J) o# q& U当我们以exp(ipx) 基底,把上图的矩阵表达式做一个简单变形时,可以写成下面这个样子:

! b3 w& u9 J) {# w4 P: c
上面这个矩阵表达式,意味着exp(ipx) 是φ(p)的微分形式的本证态。也就是说,在微分形式下,平方指数(非线性)形式的高斯函数可以转化为以exp(ipx)为基的线性结构。 & d' ?- J5 X, F9 W$ N
 / l+ Z$ y0 m. Y- w; |$ G) t' R, s / l+ Z$ y0 m. Y- w; |$ G) t' R, s
8 f. W4 L- z8 g N7 X光滑图形通过微分构造出的这种‘微分形式线性关系’,正是微分几何。微分几何特别关注弧线,它把非笔直的弧线每个微小部分看作一段一段的微小直线段,然后在多重直线段模式下,进行多重线性分析。微分几何的实质,是把有限维欧几里得空间的维度扩展。比如把x坐标轴,扩展为dx1坐标轴、dx2坐标轴、dx3坐标轴......dxn坐标轴等等为新坐标轴的无穷维度空间。原本欧式空间x坐标轴下的曲折蜿蜒的弧线,在新的‘微分基矢量’dx1>、dx2>、dx3>......dxn>下变成了‘微小直线段’的组合。这样,有限维的欧式几何扩充成了无穷维的微分几何,非线性的曲线转换成了微分形式‘线性空间’,于是非线性关系变成了线性关系(或者多重线性关系)。显然,以微分dx1>、dx2>、dx3>......dxn>为基矢量的无穷维空间,对应于“连续无穷维矩阵”。
5 a; b# G0 f* S9 N/ C& @
7 c7 j3 K1 f! Y' j8 n. D
另一方面,我们从第三节知道exp(ipx) 函数也可以看作无穷维空间的基,比如exp(ipx) 是高斯波包的本证态。 不仅如此,傅立叶变换理论已经证明exp(ipx) 还是所有线性时不变系统的共同本征函数(本证态)。
; q. |. p! X- a- v
【定律】exp(ipx) 是所有线性时不变系统的共同本征函数系 [3] 1 |7 s* J* `( Z( G N
【证明: 设L是任意线性时不变系统,v是输入,w是输出
$ J' }7 T) u/ M* ~. z即 w=Lv
则 w(x)=h(x)*v(x) ,即w可以表达成h和v的卷积 上式傅里叶变换记为: W(s)=H(s)V(s) 如果输入exp(ipx) [注:为方便表述,exp(ipx) 省略了常数项2π ] 即 v(x)= exp(ipx) 因为exp(ipx)的傅里叶变换等于脉冲函数δ(x-p) 则输出:W(s)=H(s)δ(s-p)=H(x)δ(x-p) [注:此处H(x)是个常数] 再通过傅里叶反变换,把上式从频域返回到时域,得到: w(x)=H(x) exp(ipx) 此处H(x)是个常数,记为c,则: w(x)= c exp(ipx) 即:输入exp(ipx) ,通过L线性时不变系统w=Lv,输出得到 c exp(ipx) 即:L exp(ipx) = c exp(ipx) [注: L作用在exp(ipx) 等于常数乘以exp(ipx) ]
' g& M* U) ]& M5 K
即: exp(ipx) 是任意线性时不变系统L的本征函数 证毕。】 4 o; G) ]) ~/ o3 e" C" h
- a+ h' c) l/ y$ a+ n/ |
既然exp(ipx) 是任意线性时不变系统的共同本证函数系,矩阵力学的所有量子态应该都可以通过exp(ipx) 本证态来表达。如果我们以exp(ipx)作为连续无穷维矩阵的元素,正如时域和频域之间的傅立叶变换矩阵那样,那么这种矩阵是不是可以完整表达所有的量子态呢?若如此,哥本哈根矩阵力学又为什么会出现“不确定性”呢?
% R4 e5 L( a2 v& Z8 B如前所述,当p或x为自变量连续取值、两两不同时,可以得到exp(ipx) 本证函数系正交基,根据第三节,我们推断完备的exp(ipx) 空间维度为阿列夫2 。也就是说,线性无关的量子态有阿列夫2之多。
这就是问题的关键,因为阿列夫2级别无穷大的元素之多,已经远远超出了平面矩阵的逻辑范畴(平面矩阵的表达范围不能突破连续实数所能度量化的阿列夫1维度极限)。因此,如果以平面矩阵(阿列夫1维度的向量空间)对阿列夫2维度的量子态进行度量,会出现不完备性。所以在单电子夫琅禾费点孔实验中,我们不得不由平面矩阵扩展到高阶张量,才可能把“实体”图形和“非实体”概率幅等要素完备表达、才可能把量子本证态p和粒子实体坐标{x}的波粒二象性结为一体,却又保持逻辑的严格一致性。 进一步分析,三维实体粒子坐标{x}的微积分与连续无穷维平面矩阵是等价的,所以三维实体空间中其微分基矢量dx1>、dx2>、dx3>......dxn>的完备空间维度是阿列夫1 。而位置算符的本征值x可以是基于exp(ipx)本证态而言的,所以其完备空间维度是阿列夫2 。因为此,平面矩阵无法完备地表达它。所以本征值x在阿列夫1维度实体空间的投影会出现概率性。这和六维度骰子投掷显示一维面情况一样。高维度属性投影到低维度空间,因为其维度不完备就会出现概率性
+ J! b8 ?" |' _, M7 p
8 i; w, o0 h! V( v# B1 h" T
& c8 |& ~/ Y5 r( D
6 A. x/ ^$ Z4 a' f, b, i4 J+ E7 Y
! h$ U" B, r0 ]% S Y
* W9 F3 I1 F8 H# ^; s
需要指出的是,对于初学者来讲,很容易混淆向量和张量的概念,特别是在有限维的情况下。7 |4 W( J& K& B- W+ U( V) ^
在有限维的情况下,张量空间的数学定义一般是这样的:
+ N& ^+ Y4 d4 `! f2 i(φ+ψ)(x) =φ(x)+ψ(x)) O7 b a4 y7 d0 U
(aφ)(x)=aφ(x)0 d8 o* g( s8 o, V4 X
' i3 N2 H' _2 j5 i上面两个式子,很容易化成下面的一个式子:
{9 s9 D% P% ?7 ~7 p) ^$ e1 ](φ+ψ)(ax+by) =aφ(x)+aψ(x)+bφ(y)+bψ(y)
3 \% H1 C! Z0 Q# l- |7 a在上式中,如果把φ(x)、ψ(x)、φ(y)、ψ(y)各看成基矢量,这不就是一个向量空间吗? 其实不然。因为向量空间(平面矩阵)是单层次线性空间,逻辑结构图如下: 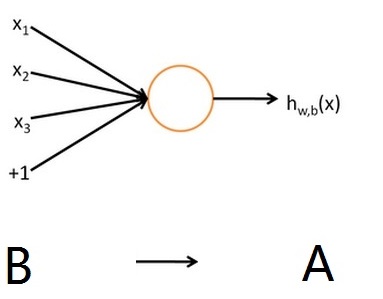
+ l2 F" N6 B; Z1 m3 y; P3 \$ M
而张量是多重线性映射,逻辑结构要复杂得多。有些特殊张量可以转换为多层次线性空间,逻辑结构图如下: 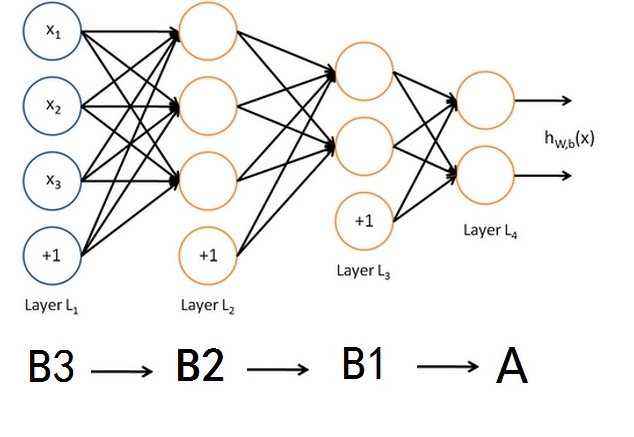
0 ^' Q4 s' ]' d0 d9 w
如果空间维度是无穷维,张量空间和向量空间更是迥然不同。 根据康托尔的理论[2],连续无穷维平面矩阵所包含的元素为阿列夫1 ^2,这还是阿列夫1 ;而连续无穷维高阶张量所包含的元素为 阿列夫1^阿列夫1,这已不再是阿列夫1,而是比阿列夫1 更高阶的阿列夫2级别的无穷大。 也正因为此,所以连续无穷维平面矩阵在量子态空间会出现不完备性。这也是平面矩阵出现不对易现象的本质。也是不确定性原理的根源。即,阿列夫1级别的基矢量对于阿列夫2维度空间的不完备性。
3 V$ D4 F% V3 V0 l
8 l2 D% d8 G+ S& T! L
+ [5 ]& J/ u4 L: C1 A! z0 c7 A+ R' K
1 }& ?" A; Y z* |- F
# h B: A. R! I; Z! N8 i2 ?& \
e' r- l! L4 h% o2 C% ]& k
=================================== 六、[命题] 相互正交的exp(ipr)函数的总个数为阿列夫2
" C) P( w/ I: ^& `, C' f* Z7 A8 v9 ~' j7 O. ]8 E1 Z O4 j
【注:首先声明上述语言表达是不严谨的,笔者本来的意思是想探讨‘在Hilbert空间定义下,以正交exp(ipr)函数为基底的系统的维度为阿列夫2’,但是遗憾的是Hilbert空间对问题所涉及的δ函数等广义函数的内积无定义、对exp(ipr)函数的内积也无定义。所以只能无奈不严谨的表达上述命题。严谨的表达可能只能等到某位数学大师扩展到‘广义Hilbert空间’以后吧。】6 ]' x+ \$ }4 i2 \, ^0 C3 [. }! H) m6 C5 `
: f3 M, N) D3 I4 t7 [" M7 Y$ o1 ~下面让我们一步一步粗略探讨,相互正交exp(ipr)函数最多会有多少个?
- N3 l/ } A7 J2 \! | M; }6 v* R E2 K(1)当exp(ipr)函数的变量整数取值时,相互正交exp(ipr)函数的个数为阿列夫0 【 证明一:9 e6 [4 m( B% S; O9 G) j* @3 H
取xm和xn ,其中m、n为整数: e1 l4 G. P! Q* d5 m
) k$ ]+ ~, W7 @$ j; }4 K) D
则:∫exp(ip)^xn exp(-ip)^xm dp ) e' F# P$ b8 {% n( q
& j7 J% `2 q0 x相当于计算两个exp(ipx)的乘积% B% E5 o5 H. Y& V; N8 N/ [
又由于exp(ipx)可以转换为三角函数:) X/ V+ d" c8 N4 ]2 ^
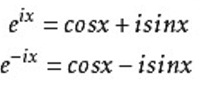 , D- i& s) h- K. J/ a# p- M , D- i& s) h- K. J/ a# p- M
2 Z6 C" W' r) @* D2 w; T: U所以exp(ipx)的正交性,对应于三角函数的正交关系
0 V+ a( i( E9 I! j5 T' t9 l0 ]3 _" {

# _; g' I$ g: h4 b. D( [
, i/ a; l: |3 M$ x' b: S . ^" C$ _3 z8 P3 u9 _ . ^" C$ _3 z8 P3 u9 _
' R; T, m a3 r- d( q, ^
即:m不等于n时的exp(ip xm)和exp(ip xn)两两内积为01 C1 \1 l: z; D& d
所以,两两不同的exp(ip)^xn 和exp(ip)^xm正交
/ a$ K- e. m2 x7 E9 b. ?又因为, 整数变量xn与函数exp(ip)^xn 对应,所以不同整数取值的exp(ip)^xn函数个数为阿列夫0
5 X1 O" } M* V9 A2 _即,不同整数取值的两两正交的exp(ip)^xn 函数个数为阿列夫0 】
- J! P* U5 @! g+ |6 S- z& L6 F/ d5 Y, P* O* u4 ~9 Z% |( V) W5 R2 F
! @# p, c" {: r3 t
5 r# w' O7 T( i
1 p5 ~+ a5 X2 t5 s# ~; J! ]" u【证明二:
* }2 R# l" z2 z) x0 H8 s% T3 S3 ?/ x' U1 d
因为8 V1 O3 e+ Y$ _& U0 [* q u
 ' t2 H3 l% K; L3 Y1 ~0 f' U% } ' t2 H3 l% K; L3 Y1 ~0 f' U% }
2 U! d3 m+ _. _根据欧拉公式:. B" K2 l# T- c- [* U! c: _ D5 q. B8 b
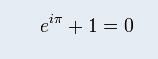
4 X! h1 ?9 d6 v4 ^) M0 D' W1 ^! S; |, \9 ~: i& w5 P8 l2 J5 R
可知,整数不同取值的 k、m的exp(ikt)函数 和exp(imt)函数两两正交
" n4 ]* \6 Q& l! X& i) S# i# s- g又因为, 整数变量k与函数exp(ikt)对应,所以不同整数取值的exp(ikt)函数个数为阿列夫0# \ l8 m- y0 k' |3 G5 }
% l0 `$ v/ N- t, Z( o, N+ e
即,不同整数取值的两两正交的exp(ikt) 函数个数为阿列夫0
9 r" f1 }( T& U* E】
$ Z8 q/ Q; h! Y% @( |! Q
( H1 ~" _4 M3 x+ q* |
& a% Q+ i8 n; N) m1 B/ o! F
' y( K2 _7 Q; [. |/ Q- N----------------------------------------, n( p5 p5 h c6 z4 c
(2)当exp(ipr)函数的变量实数连续取值时,相互正交exp(ipr)函数的个数为阿列夫13 d: O) k. b3 @- A$ a6 ?6 G7 e ?
【证明如下:
/ R" W. b& e) |3 [7 t
2 i: R) x! ?! b& u! [- C+ G) ]& f1 B
& D5 t- Q6 r1 }可知,连续不同取值的x的exp(ipx)函数两两正交" S* s2 N- a/ z0 u/ f5 u
由于连续实数集合的势为阿列夫1 ,即两两不同 x和x'个数为阿列夫1$ Q1 B2 S: G# A1 ?+ X) I
又因为,任意 x'变量 映射到不同的延时δ(x-x')函数
$ x* B$ P2 V$ R3 k0 v# L所以,连续不同取值x’时,两两内积为零的exp(ipx)函数个数为阿列夫1
/ q f( c( x3 u即,两两正交exp(ipx)函数个数为阿列夫1 】3 }( S; R1 R4 |6 t# P/ B
+ D' ^: C) D! {0 u2 s+ F o) ?. D9 u. z; y- H$ q
1 L1 L! @3 h" y' E. b
【注:上面这个证明对于Hilbert内积空间而言是不严谨的,因为exp(ipx)不是平方可积函数、不存在于Hilbert内积空间。但是基于下面两个事实,判定变量x连续不同取值的exp(ipx)函数两两正交并无不妥:
3 D& e& W# E, V9 Q/ a/ m. v- I' z' S9 G
7 `/ ~3 T& B/ p" h$ F- {4 q) @ V
第一、exp(ipx) 是某类线性系统的基底 [定律:exp(ipx) 是所有线性时不变系统的共同本征函数系 ]
! f9 h/ m/ a: W8 _ [证明: 设L是任意线性时不变系统,v是输入,w是输出 即 w=Lv 则 w(x)=h(x)*v(x) ,即w可以表达成h和v的卷积 上式傅里叶变换记为: W(s)=H(s)V(s) 如果输入exp(ipx) [注:为方便表述,exp(ipx) 省略了常数项2π ] 即 v(x)= exp(ipx) 因为exp(ipx)的傅里叶变换等于脉冲函数δ(x-p) 则输出:W(s)=H(s)δ(s-p)=H(x)δ(x-p) [注:此处H(x)是个常数] 再通过傅里叶反变换,把上式从频域返回到时域,得到: w(x)=H(x) exp(ipx) 此处H(x)是个常数,记为c,则: w(x)= c exp(ipx) 即:输入exp(ipx) ,通过L线性时不变系统w=Lv,输出得到 c exp(ipx) 即:L exp(ipx) = c exp(ipx) [注: L作用在exp(ipx) 等于常数乘以exp(ipx) ] * l K* N* H1 O8 P3 G
即: exp(ipx) 是任意线性时不变系统L的本征函数 9 N, \: H. E# {3 d) t: z b2 C
, g' b; y9 r. v' ]) M! O
第二、exp(ipx) 满足狄拉克正交性质
F3 r7 v1 P: V4 U3 d) M( t: ?; z! ]( p6 S* D0 J3 e* d r" u$ G+ X
 4 l8 Z h5 a3 ]( w 4 l8 Z h5 a3 ]( w
6 A- z. D! P$ S
】+ J8 G, P# d) d5 |0 d
7 A+ R( A6 z* V
. O* w: b% s4 G& a- m! `+ U9 `- K1 K }0 f, A: M
-----------------------------------------
9 a" d* ~! ]' x6 Q3 n5 ?
+ E4 D1 B4 a+ n/ Q4 s(3)当exp(ipr)函数的变量完备取值时,相互正交exp(ipr)函数的个数为阿列夫2: x) J4 ^) f: I; H1 I9 y
7 \% k7 _% k0 I# z
【探讨:
/ n9 N, Y3 } i6 s9 Y( q2 a(步骤一)- F5 ~( R& D3 l v: C% ]
根据:
& ^, ]" y$ q3 a5 }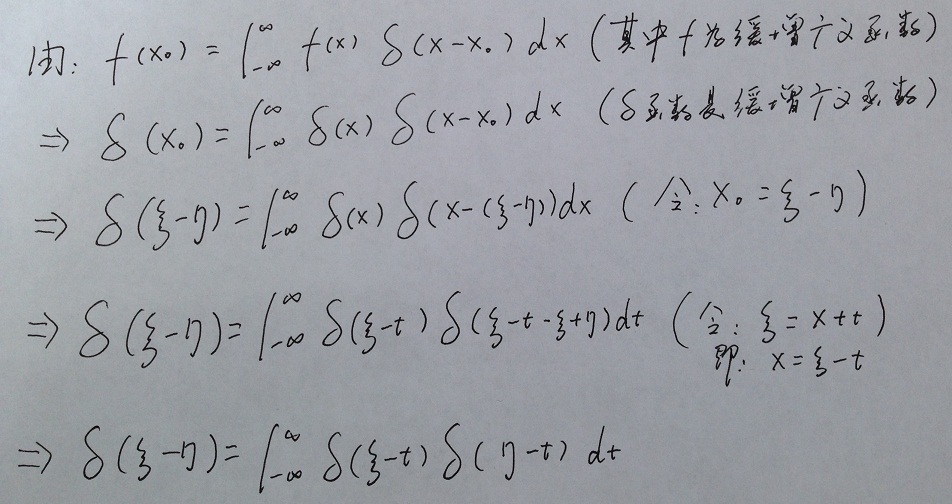 5 T3 }5 d# O* M, i5 L# P5 c4 i 5 T3 }5 d# O* M, i5 L# P5 c4 i
得到:7 Y4 w a2 x& y+ B4 Z. J s
 . g! e% Y$ k2 z9 I* U! V . g! e% Y$ k2 z9 I* U! V
【注:上面这个证明对于Hilbert内积空间而言是不严谨的,因为δ函数等广义函数不是平方可积函数、不存在于Hilbert内积空间。但是基于下面两个事实,判定变量不同取值的δ广义函数两两正交并无不妥:: K% s% I( V* g' R' }" u/ p
) Z" w7 u; Y/ w
6 `4 |% H) }0 k, e4 v: b- ]& M 第一、δ广义函数是某类线性系统的基底6 I6 E$ ?# {9 b# U
' R5 W, G$ F6 o( T# W1 F[定律:δ广义函数是所有线性时不变系统的共同本征函数系 ] ! i- |$ a8 u! ?3 ]4 B6 i# Q
[δ广义函数和exp(ipx)函数一样,都是基元函数,都是线性时不变系统的本征函数]
* G+ m! j0 C, ~# J[在实际应用中,延时δ函数常常作为连续无穷维积分空间的基底,提取相应微分分量特征值,即取样:7 r4 W. d- J- y; H! O
 . |; x, ^# R K$ S1 q . |; x, ^# R K$ S1 q
/ ]: D1 ~. R9 ]$ Y2 L5 ?4 \9 ?# p, x% J+ d$ j# o1 |( u V
3 x2 i. G# b8 q! m1 T
第二、不同延时δ(t-r)函数的乘积积分 与通常意义的内积的正交性质不冲突5 I" ~0 {# u- m( A8 S$ ]
- e4 X6 i3 \& L1 q0 t[ 说明: D2 q z! A6 A! D8 b- ]' x- H
实数变量的函数可以看作连无穷维向量,因此可以以向量形式分解函数,以西格玛类比积分2 d! c% V, m7 z0 m% o( G
∫δ(t-r)δ(t-p)dt 如果形象类比离散的西格玛符号形式,如下: ∑δ(tn-r)δ(tn-p) = 0+0+0+......+ δ(r-r)δ(r-p)+......+ δ(p-r)δ(p-p)+......+ 0+0+0..... ) U! o3 E0 n! ]1 W ]7 m0 @
即,当tn<>r(或tn<>p)时,各分量均为零 即,仅剩tn=r(或tn=p)时,分量δ(r-r)δ(r-p) 和 δ(p-r)δ(p-p) 可能不为零
G2 V! d; w* C% c' ^又因为,δ与x 的分布积等于零,即 x δ(x)=0 所以,δ(r-r)δ(r-p)=0 δ(p-r)δ(p-p)=0
' a" @, w: @! d2 { c+ ^3 q9 M7 p) l0 O% S. r+ i y5 f
所以,∑δ(tn-r)δ(tn-p) = 07 e, Q( i* ?3 \9 h! `
: Y: G* v: i7 ]4 t) m$ ?( k
b6 L% b( z, p% d/ v( D" Z】
" Y8 f! m& _. e0 E2 T H5 Y/ H# q& j; c, b6 x8 ?/ u, f
! n6 B0 T1 f! X
$ C& K J5 }, q; z% p
% p% ?' Z/ K0 ?3 E! c' N' u5 m) J
(步骤二)/ _: P* Q0 x% @4 e
! v, S5 c, m4 E6 k: P因为在坐标r表象中,动量p等于(-id/dr),即p为r的函数,记为:p=f(r)
$ P- m8 K! Z- {: R) h0 @因为动量p确定时,p=f(r)是一个有限值,此时坐标r取值范围是从-∞到+∞ ,此时如果p×r空间集合全体元素与实数集满足一一映射,则p和r之间满足不动点定理。1 n- t, t# g+ I% S
4 ~( a( C, @' I即,如果p×r共同空间的全体元素与连续实数空间点可以一一映射,根据实数稠密性不动点定理,则存在r0,使f(r0)=r07 P1 z) h" P* e! W0 @' ?
. H6 U, ] v9 s* o) v* ^ g
即有,p0=r0 ,这意味着动量和坐标可以在某一点同时确定。这与不确定性原理矛盾!
0 b1 \, s4 L4 ~- Y% I: ^
9 u# Z" s! d$ L* D所以,p×r共同空间集合全体元素与实数集合不满足一一映射。, R$ \4 C" R0 ~/ D7 ^0 u; N$ z
! ~/ g+ I' ^# E8 A3 b
. D: N+ h5 ^! q1 P ~所以,p×r共同空间互不相等元素的集合的势不等于阿列夫1: \, J. o* e5 s- z) `: `, R
又因为p×r共同空间的r和p可连续取值,所以 p×r共同空间互不相等元素的集合的势大于阿列夫08 X3 K8 `0 V( l/ M6 {8 g
所以,p×r共同空间互不相等元素的集合的势大于阿列夫1
U) d4 e; E. p w# F' n( U$ P( o
, N0 P2 y! Y0 E$ x Y* l7 d/ f8 K% b4 [8 Q: H" L8 ?+ w
9 d% x# E# m; f5 h$ N$ O4 d6 _+ M$ S8 @% h) P% p
即,互不相等r、p的元素个数大于阿列夫1 `4 y1 p2 g8 }: w0 W0 o
即,互不相等r、p的元素个数大于等于阿列夫2
6 F4 C: y% P/ \【注:+ E: Q( H) l' P$ v m4 s
1、根据不确定性原理,频域和时域不能同时为压缩到点值:
- Q x7 e3 l- \9 Q: ]" D1 W4 f( F& D/ J: e. G: s2 s7 i

R6 H" ]& T) ^! R2 `( Y8 l u- N; L6 G2 A
' j; x* o1 ?( g# ?) J0 k9 ?' d
6 m. e1 ]* }1 v! K) _: n; ~$ o
& x: g# k4 G$ }9 T! v
2、当动量p为确定值时,坐标r在-∞到+∞之间震荡,r在每一个具体位置的平均概率为零
- ?' G% l1 a! l& ]3、 根据“单电子夫琅禾费点孔衍射实验”,夫琅禾费衍射分析的量子现象类似贯穿势垒的量子隧穿效应,具备某能量(频率)电子将会闯过障碍“点孔”、另一些则穿不过去。这对于单个电子而言,相当于逻辑上的概率性,而这种表征不同频率的电子的穿透性的概率幅,表征了‘概率本证态’。只有在线性时不变系统表象中,对单电子夫琅禾费点孔实验的 “单电子”、“点孔”和量子隧穿效应的“概率幅”等要素才能做到一一对应完整表达。在傅立叶变换下,经典物理实体动量{p}由一个点值将扩张成了对偶域的一系列概率本证值r21、r22.....r2n等。在量子力学中的量子态的意义不仅仅局限于实体坐标,还包含了‘概率本证态’等新要素,‘概率本证态’的意义比实体空间含义更广泛。( Z1 F/ e9 c3 J! Y g$ ^' L% F
4、经典力学中在实体空间中讨论矢量关系,所涉范围为向量空间(即矩阵),经典力学的的实体空间与连续无穷维矩阵是一一对映的。 但是,平面的矩阵无法完备表达‘概率本证态’。详见:[命题]矩阵力学的高斯函数的exp(ikx)本征函数系不完备- P+ g4 l3 _; p" [3 F% l
5、完备的“概率本证态线性时不变系统”是一个高阶张量,是多重线性映射。这种多层次多重线性映射,比单层平面矩阵复杂得多,因此包含了更多的线性无关的基底。
m8 K$ X& T- f) ^% O; E】2 h) H$ H' Q8 s- F0 a
# ^5 U- D5 h$ {: m: B' j
9 N+ m# u9 j9 \: o% a, H1 m8 X0 G T5 k) t! W# e6 W1 v
2 T1 b0 g" A# `1 Q(步骤三)
- J! n6 ]3 p5 G8 d: H. y6 z. L! m; z/ s
互不相等r、p的个数等于δ(r-p)为零值的个数,根据步骤一,δ(r-p)为零值的个数等于δ(t-r)和δ(t-p)相互正交函数的个数 p% O0 @' i5 ]& o) H3 Y
根据步骤二,互不相等r、p的元素个数大于等于阿列夫2,所以δ(t-r)和δ(t-p)相互正交函数的个数大于等于阿列夫2
: G- _8 w5 B& E$ b9 o: V6 C
3 h& T3 M$ }# B9 Z7 C即,两两正交的δ(t-r)、δ(t-p)函数集合的势大于等于阿列夫29 w. j& J% N, |$ }) q! R3 z
即,全体δ(t-r)函数集合空间的维度大于等于阿列夫2
. j! X# L; ^) t- }% k% P$ C1 A7 S: @
+ t/ B7 Z9 x* D, F
& U" C' Y4 d- G6 x. A
! d3 C5 D( `/ v1 P+ K* h8 ?, i (步骤四)' b" J& C' h0 r' Q0 w
因为:
" [' E* {# _6 C; _ . \" u% A- B. k- K4 j" g- t1 m . \" u% A- B. k- K4 j" g- t1 m
{& F! C% F4 ~: P2 B
即,傅立叶正反变换均不是一对多的映射+ J4 \) Y2 ~, T2 \( r8 F7 H
即,傅立叶变换非退化,是非退化的线性变化# ~: f/ y" k+ _: A9 |! D$ j
7 R6 S: N6 Z( m M
! {' T4 I; ~2 `& E6 \3 z) ~0 R(步骤五)
/ A6 `+ g" U& ]2 G# s2 U& |因为:
# A0 s2 n; c) h" Z, S/ Y ~
0 u: D3 y7 c& k% J9 c: v
6 M3 u& C0 l% R0 ~即,基元函数δ(r-p)和基元函数exp(ipr)是一一映射
: S+ O8 E( D% T9 I
9 c+ ]5 p+ @5 o9 V$ z* n9 {( L Q' S9 N# h. r" p( v$ l
(步骤六)
: `) A9 [, a4 y5 y h根据步骤三和步骤五, 全体exp(ipr)函数集合空间的维度大于等于阿列夫2& K( s6 O4 j% D8 \" ]
) L# D4 L% B- Y! Q" A
/ {& y/ U3 `9 \3 j7 g+ ^6 B! Z(步骤七)
$ C6 J/ E, n0 \# Z. \又因为:
% }1 X0 Z" A- W/ R 0 u/ i3 C6 @0 n 0 u/ i3 C6 @0 n
, f/ W7 S# Q/ o0 S1 t/ T0 r【注:阿列夫级无穷大是对集合中元素个数的评估,如果按照某种一一映射规则把集合元素按有序集排列,当最大元素映射值不超过阿列夫2 时,则集合元素个数不超过阿列夫2 。量子态空间可以考虑把系统能量(哈密顿算子)作为排序映射规则,此时坐标表象中最大排序元素映射值不可能超过阿列夫2 】
; |: }: K. i- o/ [0 [
1 b" m' \7 M+ T- G# R
/ Z5 s" Q1 B# W( y8 \$ E" m' P
k+ u# p3 F5 r M7 C, V(步骤八)" ^! c' t9 } Q' o/ P1 p6 u
根据步骤六和步骤七,因为空间维度不大于空间元素个数。
( N2 d2 t* b; S5 U6 M6 J) w所以, 完备的exp(ipr)函数集合空间的维度为阿列夫2
; u' Z) |- U( f2 L. Z7 [5 F# V+ B; ?! N" Z- b
7 e0 b& g0 S- i1 Z& |6 j
3 t* ?7 }: V0 P3 }+ o- v
证毕。】
$ R5 b' K; K3 i8 A, {
6 B5 ^+ \9 Z7 G: w& n" N1 a
* ~: }" K. E6 t$ ~, f* j1 p
七、冲激函数δ与 实无穷 阿列夫1维度向量空间,在表达阿列夫2维度量子态空间时的局限性,还体现在冲激函数δ的刻画。冲激函数δ是单位1的傅立叶变换,同时冲激函数δ的傅立叶变换是单位1 :
2 ~4 s8 L1 U7 b% Z6 J$ R4 l3 y- c5 f
' }$ w! V3 D6 e: y5 ?2 c# |
, ~; G% I/ Y( v# v) I4 H0 W0 q形象而言,冲激函数δ在阿列夫2维度的态空间相当于单位1,其重要性是不言而喻的。, [% S! D7 ~& N- s8 n8 x5 G
但是,如此重要的冲激函数δ,其数学定义却是异常怪异的。它的定义是这样的:
' w0 A& T9 S% V1 K0 ]) ]
2 B9 t& g; s6 C. Q/ @- `
冲激函数的应用取得了巨大成功,甚至可以说如果没有冲激函数就没有量子力学、信号学、傅立叶变换。但是冲激函数却让数学界异常窘迫尴尬,数学根本解释不同这是个什么东西。
j' @/ ^ [/ S因为这个怪胎函数仅在0点一个点有值、这个点值是∞、其积分等于1 (积分宽度为0、高度为∞、面积是1),; x9 M) W4 H! S# ^
数学表达为: 0 × ∞ = 1 。: o/ _/ F; J' `# Q! K
零乘以无穷大等于1,放在严谨的数学体系中,谬误很明显。
1 A" Q* e8 `* C2 z因为这相当于1/0= ∞ ,意味着两个“确定的”数的算术运算将等于“不确定”,这在数学逻辑中完全无法解释。) U- c2 S+ Y1 I' K% J; @2 b* K0 I I
但是,在阿列夫2维度的态空间中,以连续实数空间定义的冲激函数δ阿列夫1无穷大,却具备普通数值的演算性质。 比如,我们熟悉的三角函数cos ,它的傅里叶变换函数存在吗?  . L8 l) V. i) }# x' Q; l$ V . L8 l) V. i) }# x' Q; l$ V
+ a( s' |. ]5 f! r$ `
如果我们以经典的微积分(阿列夫1维度)理论来观察,会发现这个积分不收敛,也就是说在实数理论中cos的傅里叶变换函数“不存在” 。3 n4 V, G0 _, P1 u7 M+ C
但是,如果基于张量空间的傅里叶变换理论,很容易可以算出cos的傅里叶变换函数(等于两个脉冲函数δ ):  & D N: U0 p1 I" u- w4 _* ?2 Z7 l & D N: U0 p1 I" u- w4 _* ?2 Z7 l
l! C |, @( i/ `: F. ?6 x( d这是工程学、信号学、物理学习以为常的图像。稍微调试一下频域的脉冲,很容易就能造出时域的cos余弦波。cos的傅里叶变换函数图像很明显是收敛的。# O) F# t. m. H8 O& X6 j
而且,cos的傅里叶变换函数是两个脉冲的确定的算式:1/2(δ(a)+δ(-a)) ,这个简单算式明白无误的表明了
/ A- }! s/ {3 G$ B2 aδ相当于普通的确定的数值(虽然它是无穷大,它却可以‘量化’而计算,这是‘实无穷’最贴切的例子)。 5 Y; b& [' F/ `% ]+ ?
* f, P# V& e m: U$ l$ M& _3 u同样的,根据实无穷理论,可以很好的解释cos的傅里叶变换函数,为什么一会收敛,一会又不收敛呢?它到底收敛吗?
. f5 n9 G) w5 K4 C9 r6 ]; V
如果我们以经典数学连续实数点(阿列夫1空间)的旧眼光来观察,会发现这个积分不收敛;但是在阿列夫2维度的傅里叶对偶空间中,这个函数收敛。进一步审视,因为当冲击函数δ处于阿列夫1的范围(实数点积分空间)时,它超出空间逻辑范围,所以阿列夫1大小的δ相当于非确定的无穷∞,它不收敛;但当冲击函数δ处于阿列夫2的范围(傅里叶张量空间)时,它未超出空间逻辑范围,所以阿列夫1大小的δ相当于某个确定的数量值,它收敛。
: p8 g4 @8 A* Y- |2 N
7 u# f! c4 K; l* p
5 J+ @2 m$ ]% s$ x+ a9 a+ Y# R/ y
8 C1 U( _$ k4 T9 ]$ J! q
: D9 d$ `1 q" X
* O& W, m/ B6 l" s* d2 l
5 U' r( ], ]2 Z6 f P# d7 U
1 M9 X/ v/ ^" n- C: n$ P
' K4 X, s: L/ w% e" T: E
" [$ z. |8 s& J
八、小结
4 g6 k: }. y) x下面再捋一捋“不确定性原理”和“不完备性定理”的内在脉络。
1、二者都是线性空间的表达引出的问题。“不完备性定理”问题的是形式逻辑公理体系问题,公理体系是基于线性空间的。“不确定性原理”也是有关线性空间的问题。海森堡的上司玻恩在阅读了海森堡交给他发表的论文后,发觉了位置与动量无限矩阵有一个很显著的关系──它们不互相对易。这里,‘不对易’和‘不确定性’互为充分必要条件。对易关系是针对矩阵而言的,而矩阵是线性系统的典型表征。 2、对易关系有一个充分必要条件:“如果两个算符有一组共同本征函数函数,而且是完备系统,那么它们对易。”可见,不对易算符的本质正是线性系统的不完备性问题。 6 ]# O$ `4 p1 k; k% ]& v) ` X
我们不难发现,‘不完备性’和‘不确定性’本质都是线性空间的维度问题。“不完备性定理”的实质是维度的不完备,“不确定性原理”的实质也是维度的不完备。 不完备性定理说明,阿列夫0级别的基矢量对于阿列夫1维度空间不完备;不确定性原理说明,阿列夫1级别的基矢量对于阿列夫2维度空间不完备。 0 ?; u5 e2 A) f0 k: z, S7 D7 @% [
1 d0 d1 [9 V2 f W
+ l/ x. @% \- Q
exp(ipr)函数内积还有更多深刻的含义: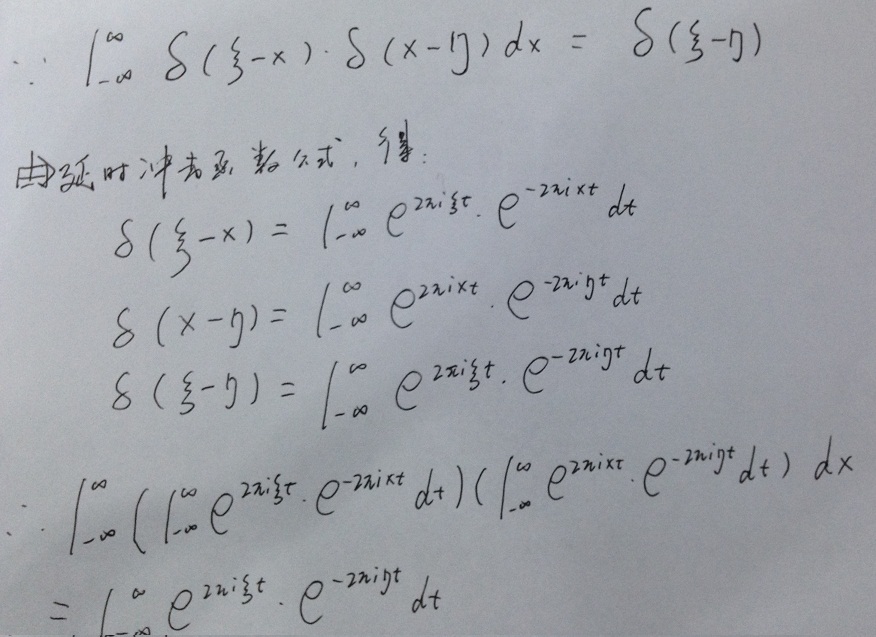 5 `" f! |1 [$ e; F! @ 5 `" f! |1 [$ e; F! @
0 c- w8 T2 }+ e8 R) ~7 o) q
! y3 h2 e& b5 \$ ~2 [9 I1 u9 j
6 m" D: q0 ~" M' @; o8 \" K6 W6 t. }' S9 @5 X/ z
. X2 c7 [; O, X8 r/ p9 ` |