本帖最后由 sunsong7 于 2015-4-21 21:32 编辑 & Q* h" Y; ^" I, u5 L3 k
: a( ?/ C) [+ r# Q( c
5.7 盖世英雄 阿列夫2
R* ^8 w6 O' S3 s' m( a: f
! [3 s5 X! ?# H8 c8 I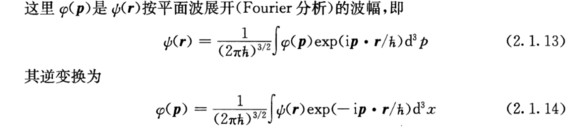
+ Y; X* o% P- K4 }6 `
I6 F8 v: h2 q; P5 x/ ^ 相信很多朋友见到这两个式子都不陌生,但是却很难亲切。因为这两个式子很容易让人迷糊晕菜、眩晕头疼。每一个坐标值都由无穷多个动量值构成、而每一个动量值又由无穷多个坐标值构成。就像在两个对照的镜子里,你中有我、我中有你,层层嵌套、无穷无尽。第一直觉很像一个无穷大的无穷大次方空间,心里不停的嘀咕,∞ ^∞ ,这是一个阿列夫2空间么?
6 L0 g4 R0 h( U 【注意:完备exp(ipx)元素构成的空间是高阶张量,并不局限于平面矩阵】( r6 H7 r; w& e- X# w. V
 % x& n+ K. V( [7 O' [- m7 u, B % x& n+ K. V( [7 O' [- m7 u, B
: }$ s& w* V% J9 e' q- p/ o* Q7 r: H! t0 b, G! ]1 c
下面是关于阿列夫2空间的一个证明。% |7 l8 S; V, M0 J
! `' z7 i1 x. r2 A% s7 Q2 y! Q I
2 K4 L$ r4 W% g7 J8 v[命题] 相互正交的exp(ipr)函数的总个数为 阿列夫24 j- { c5 V9 r% d
: F# [6 s. E/ J: H: o T/ f E6 ?1 ^7 [. D
1 V' E& M, q- B# j' H! m$ X【注:首先声明上述语言表达是不严谨的,笔者本来的意思是想探讨‘在Hilbert空间定义下,以正交exp(ipr)函数为基底的系统的维度为阿列夫2’,但是遗憾的是Hilbert空间对问题所涉及的δ函数等广义函数的内积无定义、对exp(ipr)函数的内积也无定义。所以只能无奈不严谨的表达上述命题。严谨的表达可能只能等到某位数学大师扩展到‘广义Hilbert空间’以后吧。】
& O' F, N9 ]8 f& |+ f6 x* r& |8 H/ U
! y: ]' Q" Y4 q+ C/ |3 h下面让我们一步一步粗略探讨,相互正交exp(ipr)函数最多会有多少个?- N( W, I; J" \% _
9 f& m8 w5 P) v' m
(1)当exp(ipr)函数的变量整数取值时,相互正交exp(ipr)函数的个数为阿列夫0
; u. E$ @. e* h. @: p【 证明一:: l( P3 _5 J6 {+ a4 w- G0 L3 R
取xm和xn ,其中m、n为整数
3 w3 m. ]& `: y% f* `# X. ?/ G7 A" Z- J1 Q/ w9 n; s( J
则:∫exp(ip)^xn exp(-ip)^xm dp
: D8 w, J+ W) I* K6 j) S
; i# y9 o ~' `8 |2 ~. ]1 S4 }相当于计算两个exp(ipx)的乘积0 c4 p3 [; p5 O, d& R
又由于exp(ipx)可以转换为三角函数:
# s$ {* v( _1 c. b. I# o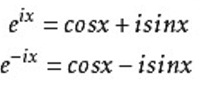 : |" a! L4 U! W1 S : |" a! L4 U! W1 S
" g: @7 Q: U& N P1 g6 X所以exp(ipx)的正交性,对应于三角函数的正交关系
% X/ u9 m+ }; u6 r
9 j" d. ^, t; V- @
4 B3 V: S! u& { m7 r1 [ * X+ }5 Y( T; ^ * X+ }5 Y( T; ^
) A9 W8 {8 ~( `) F5 M即:m不等于n时的exp(ip xm)和exp(ip xn)两两内积为0
' [/ H+ V# t) A2 l' c所以,两两不同的exp(ip)^xn 和exp(ip)^xm正交
$ Q) g9 p5 ?. V* j& Q9 s, C2 Y' s又因为, 整数变量xn与函数exp(ip)^xn 对应,所以不同整数取值的exp(ip)^xn函数个数为阿列夫0' G, h! i+ r# I$ u V
即,不同整数取值的两两正交的exp(ip)^xn 函数个数为阿列夫0 】
- i* ~3 y" i% i. \( T$ A: V3 R; F5 @9 Q a
; q' d {3 C7 X" d* x
3 i8 ?. G; a' G$ W% y
4 ^; E+ r) Y& n3 a【证明二:
6 v" G& m+ V, q" R$ [
% Z! i* A% b( J2 S6 T$ @因为3 | B0 m8 r; G1 t* M, @4 w' G9 u
 , `' s: G8 b! v0 P3 g , `' s: G8 b! v0 P3 g
% F3 O( ~0 |+ _
根据欧拉公式:
( I) S O3 O7 o( |4 M# w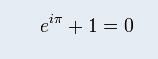
$ f7 X- i$ P& q8 x c/ b* W) X. W) K' R/ x8 ~/ J: N0 p. ^3 f
可知,整数不同取值的 k、m的exp(ikt)函数 和exp(imt)函数两两正交9 }5 P. p$ b! R3 J# |) N
又因为, 整数变量k与函数exp(ikt)对应,所以不同整数取值的exp(ikt)函数个数为阿列夫0
& p6 S; x) `5 V9 |" Y; r
& s) |' D+ I6 [& W即,不同整数取值的两两正交的exp(ikt) 函数个数为阿列夫0 】
0 k6 |- I! ^# d ^
7 U7 x1 m& |/ H/ C' i- R' `( G. O, y( E) ~) o
( ~) W M+ x6 a6 o& f; ^, N, O( b----------------------------------------/ D7 H& e+ r; B# K
(2)当exp(ipr)函数的变量实数连续取值时,相互正交exp(ipr)函数的个数为阿列夫1
2 @& R+ v7 v& L【证明如下:7 E$ P- h3 ?* }8 l/ ?. p& H% K, E

1 V/ @( `% l4 p6 S, O) ` D( A$ I2 {1 _! j% ?8 s$ B2 C3 @
可知,连续不同取值的x的exp(ipx)函数两两正交
5 y/ u; R% S* \/ D$ g9 m. {由于连续实数集合的势为阿列夫1 ,即两两不同 x和x'个数为阿列夫19 s, q a' ^) W
又因为,任意 x'变量 映射到不同的延时δ(x-x')函数% | ]) O! B4 d9 O. Y1 Y
所以,连续不同取值x’时,两两内积为零的exp(ipx)函数个数为阿列夫1
/ Q) K/ F& C3 K2 S9 ^即,两两正交exp(ipx)函数个数为阿列夫1 】
- ^1 R; d% ]) z% [& j
1 b2 e- ]2 u- s1 V q0 H/ G; g( O0 G( O& `2 _! J
5 N3 K1 r D9 Y v4 F
【注:上面这个证明对于Hilbert内积空间而言是不严谨的,因为exp(ipx)不是平方可积函数、不存在于Hilbert内积空间。但是基于下面两个事实,判定变量x连续不同取值的exp(ipx)函数两两正交并无不妥:1 @# o4 v2 p4 K2 ?- c! r
T+ ^, ~. N3 J* b8 i7 j # B4 i2 x9 z; Z7 C) x- d5 C
第一、exp(ipx) 是某类线性系统的基底 [定律:exp(ipx) 是所有线性时不变系统的共同本征函数系 ]
9 v5 j# L0 P3 B5 Q% k+ w8 F [证明: 设L是任意线性时不变系统,v是输入,w是输出 即 w=Lv 则 w(x)=h(x)*v(x) ,即w可以表达成h和v的卷积 上式傅里叶变换记为: W(s)=H(s)V(s) 如果输入exp(ipx) [注:为方便表述,exp(ipx) 省略了常数项2π ] 即 v(x)= exp(ipx) 因为exp(ipx)的傅里叶变换等于脉冲函数δ(x-p) 则输出:W(s)=H(s)δ(s-p)=H(x)δ(x-p) [注:此处H(x)是个常数] 再通过傅里叶反变换,把上式从频域返回到时域,得到: w(x)=H(x) exp(ipx) 此处H(x)是个常数,记为c,则: w(x)= c exp(ipx) 即:输入exp(ipx) ,通过L线性时不变系统w=Lv,输出得到 c exp(ipx) 即:L exp(ipx) = c exp(ipx) [注: L作用在exp(ipx) 等于常数乘以exp(ipx) ] 5 K/ A) R8 P! I. w
即: exp(ipx) 是任意线性时不变系统L的本征函数
& i- {, A4 n( D+ ~( i) h
8 |" v- l+ a: c) g" D. P3 q第二、exp(ipx) 满足狄拉克正交性质
# c; j' Y" h! ]( U8 p9 A# K: F; O. s& p, N9 y

' \" }, P1 Q2 e! K# B% l
9 L9 B# `1 t6 o+ Y: [/ H) \# n% [" K: R9 J4 n2 A
# x/ } }$ t) a" |5 m
4 v( Q5 |: ?; p. `! f; [
% z5 z3 v4 _* L8 S1 G& o-----------------------------------------
9 P+ N2 n8 e, v% F' ^# N1 \$ ? r- a' i( p2 K% n7 f- s a2 h
(3)当exp(ipr)函数的变量完备取值时,相互正交exp(ipr)函数的个数为阿列夫2
/ i" e9 r% r2 ]' S$ ]2 G5 J
% f! _1 F" ^/ H6 J! S! Z4 P【探讨:
- \/ N7 |. N$ e* s9 t% W(步骤一)
1 v9 \8 F. X7 s0 K& o, y8 r- V根据:
5 c, h* f7 m! s) W& u5 f5 r2 j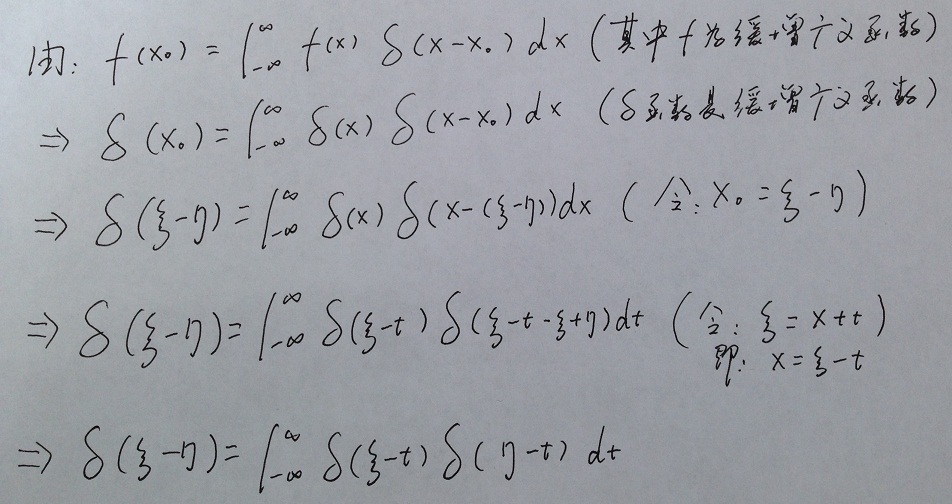 3 H& a" r4 \9 J: C' v 3 H& a" r4 \9 J: C' v
得到:
" i E+ z# g$ w ) G/ G# T( r' H- n/ B2 \# l) j ) G/ G# T( r' H- n/ B2 \# l) j
【注:上面这个证明对于Hilbert内积空间而言是不严谨的,因为δ函数等广义函数不是平方可积函数、不存在于Hilbert内积空间。但是基于下面两个事实,判定变量不同取值的δ广义函数两两正交并无不妥:
; p3 Y. y# ?, X" [
. X! q# t2 ?" M+ B- V( L. [ h: O n5 L1 z. e* [$ j' t+ Q9 e
第一、δ广义函数是某类线性系统的基底
' _2 F. L$ J& v/ N' b
% |0 H5 \+ ^9 S- y[定律:δ广义函数是所有线性时不变系统的共同本征函数系 ]
; v& |0 R# X1 @9 N" m[δ广义函数和exp(ipx)函数一样,都是基元函数,都是线性时不变系统的本征函数]
# L: S' V1 d! a& k' O[在实际应用中,延时δ函数常常作为连续无穷维积分空间的基底,提取相应微分分量特征值,即取样:( V8 M& |% U# c
 5 C4 t7 i+ m( S W 5 C4 t7 i+ m( S W
% y: i# P* b8 O* ]; g( w [
9 S, ?' s+ t* M2 _. y. o
4 l9 K6 W8 R: ~4 b
7 A' [: l: n0 r x( h, {
* z3 \' f& M$ i' i3 p第二、不同延时δ(t-r)函数的乘积积分 与通常意义的内积的正交性质不冲突& s F6 R- {* P5 \
- ?5 `+ {+ b( N$ D7 J5 C* W[ 说明:
0 z8 \4 W7 r! S4 g- q% {0 H实数变量的函数可以看作连无穷维向量,因此可以以向量形式分解函数,以西格玛类比积分$ w1 A9 G* H* R. @7 r) s- p8 |6 `: e
∫δ(t-r)δ(t-p)dt 如果形象类比离散的西格玛符号形式,如下: ∑δ(tn-r)δ(tn-p) = 0+0+0+......+ δ(r-r)δ(r-p)+......+ δ(p-r)δ(p-p)+......+ 0+0+0..... 3 |1 w; Q% A/ F* g: M1 r$ |
即,当tn<>r(或tn<>p)时,各分量均为零 即,仅剩tn=r(或tn=p)时,分量δ(r-r)δ(r-p) 和 δ(p-r)δ(p-p) 可能不为零
" E7 ?! G+ ^1 ]! I又因为,δ与x 的分布积等于零,即 x δ(x)=0 所以,δ(r-r)δ(r-p)=0 δ(p-r)δ(p-p)=0
2 h4 H0 K" k8 `7 {* e& A% R: D" \
* Y" k! K' a1 X& f9 @/ ~所以,∑δ(tn-r)δ(tn-p) = 0
1 G7 m. J1 s/ _( |1 j6 D2 d& |4 e; m$ |. F7 ]0 Z* g
】
: N2 U. i0 r5 a/ X* a* @8 g [/ q* q5 x/ i
; x9 Q a1 i; f$ h9 y7 `7 }, V% ^" U
; s- M& e2 S7 c" Z6 f(步骤二)
0 P1 A2 f- p0 v* \; y" z' z- l" ~# T! k2 G" A1 [
因为在坐标r表象中,动量p等于(-id/dr),即p为r的函数,记为:p=f(r)
; `7 p6 u7 t. Q# D7 s因为动量p确定时,p=f(r)是一个有限值,此时坐标r取值范围是从-∞到+∞ ,此时如果p×r空间集合全体元素与实数集满足一一映射,则p和r之间满足不动点定理。" w" T! l& Q" t) L
即,如果p×r共同空间的全体元素与连续实数空间点可以一一映射,根据实数稠密性不动点定理,则存在r0,使f(r0)=r0
- \$ p6 U$ r1 h6 h) L1 O: x
- r5 T0 K/ l) [即有,p0=r0 ,这意味着动量和坐标可以在某一点同时确定。这与不确定性原理矛盾!6 z! y$ l9 q1 _1 S
! [4 n$ Y8 l) C! G2 B. t
所以,p×r共同空间集合全体元素与实数集合不满足一一映射。7 @/ E8 \9 S$ g9 B; @6 ]+ I
( W/ U( k" B2 Y% V
9 ^( q' I$ p+ o所以,p×r共同空间互不相等元素的集合的势不等于阿列夫1
2 l0 c6 _) j$ M又因为p×r共同空间的r和p可连续取值,所以 p×r共同空间互不相等元素的集合的势大于阿列夫0
, Y# F! c5 l. p所以,p×r共同空间互不相等元素的集合的势大于阿列夫1
) Y3 {& B5 c1 v/ n) Z/ y7 t3 r2 @
7 O+ K5 u( k+ B8 u即,互不相等r、p的元素个数大于阿列夫1
" Z5 g2 A3 @3 t# D: L即,互不相等r、p的元素个数大于等于阿列夫2
- i. J( n2 l3 A* u- c5 u【注:
+ ~3 ?3 R$ H# N& `; u、根据不确定性原理,频域和时域不能同时为压缩到点值:
7 U, o. n1 s, {% }) i
' @* g0 S/ S+ C. e$ M+ D( f1 r6 s4 k
/ L. b( s6 |, M9 r8 w1 t$ i
2、当动量p为确定值时,坐标r在-∞到+∞之间震荡,r在每一个具体位置的平均概率为零& u4 g3 F. z9 w; I! J3 _
3、 根据“单电子夫琅禾费点孔衍射实验”,夫琅禾费衍射分析的量子现象类似贯穿势垒的量子隧穿效应,具备某能量(频率)电子将会闯过障碍“点孔”、另一些则穿不过去。这对于单个电子而言,相当于逻辑上的概率性,而这种表征不同频率的电子的穿透性的概率幅,表征了‘概率本证态’。只有在线性时不变系统表象中,对单电子夫琅禾费点孔实验的 “单电子”、“点孔”和量子隧穿效应的“概率幅”等要素才能做到一一对应完整表达。在傅立叶变换下,经典物理实体动量{p}由一个点值将扩张成了对偶域的一系列概率本证值r21、r22.....r2n等。在量子力学中的量子态的意义不仅仅局限于实体坐标,还包含了‘概率本证态’等新要素,‘概率本证态’的意义比实体空间含义更广泛。
J; Y6 ^9 w9 @$ l6 z" }# Q6 l9 U4、经典力学中在实体空间中讨论矢量关系,所涉范围为向量空间(即矩阵),经典力学的的实体空间与连续无穷维矩阵是一一对映的。 但是,平面的矩阵无法完备表达‘概率本证态’。详见:[命题]矩阵力学的高斯函数的exp(ikx)本征函数系不完备
- E0 g7 [; |8 g, N6 f3 _- u5、完备的“概率本证态线性时不变系统”是一个高阶张量,是多重线性映射。这种多层次多重线性映射,比单层平面矩阵复杂得多,因此包含了更多的线性无关的基底。+ Z! ~: Z8 ~6 U7 M9 {: F
6、更多细节探讨请见后面的章节:“关于不完备性定理和不确定性原理的探讨 (小结)”】" ~+ ?: {: i. i, u
3 m! p" p, u6 F( R
* i M7 | P8 ]6 W4 n1 U# I(步骤三)
! v& a3 q" o3 Q3 K1 z
! O7 V5 L& X% ?3 F Q) l互不相等r、p的个数等于δ(r-p)为零值的个数,根据步骤一,δ(r-p)为零值的个数等于δ(t-r)和δ(t-p)相互正交函数的个数. T6 z3 R- e& l. T; Q/ V) b7 I
根据步骤二,互不相等r、p的元素个数大于等于阿列夫2,所以δ(t-r)和δ(t-p)相互正交函数的个数大于等于阿列夫2 x% G# C- |7 q3 [
! m/ q' l z& f+ o0 N8 N即,两两正交的δ(t-r)、δ(t-p)函数集合的势大于等于阿列夫2# b, C# R/ ]9 I8 O9 r
即,全体δ(t-r)函数集合空间的维度大于等于阿列夫2) C4 C6 ?- g6 U* Q
: j* G5 \* I; b; V& x: d) C: \1 T4 e1 Y6 m) Z
(步骤四)
1 T1 j! i1 _- \5 r因为:
9 ^7 q. y/ a) c8 A- w3 M* E( B4 J : U; E- m1 L7 h5 u; ]0 G$ r( K& R : U; E- m1 L7 h5 u; ]0 G$ r( K& R
+ c- U, _ w( f2 z; j
即,傅立叶正反变换均不是一对多的映射" \. G% ^3 z- z W9 O8 x4 h( x
即,傅立叶变换非退化,是非退化的线性变化
' Z, l& E( b, Y8 W0 z(步骤五)' N5 h$ K. w* V7 V M% M3 Y& ?9 k8 @4 M
因为:
$ J+ \7 V% O$ q% y' `9 v4 p3 f) T# O! `% Z

. [# v9 f' A+ o5 J1 e即,基元函数δ(r-p)和基元函数exp(ipr)是一一映射
2 ]2 n( n& w5 W( B. b0 T9 \- [; p6 p/ K+ g. F- Y3 i2 w' q
- l* _: J: R! |$ T* Y# @! k6 ^) n
% d8 p5 S3 O, ^4 \7 c(步骤六)2 g" ^5 J5 Z2 r% _& i% e7 H
根据步骤三和步骤五, 全体exp(ipr)函数集合空间的维度大于等于阿列夫2
& ]( E/ C( I7 y# k! Z(步骤七)
8 b( W6 d5 z$ P' B$ i0 y5 U. U又因为:
0 [, H& ~1 P) i5 H6 U' S3 u! X
* D2 L/ K' ]0 h( j3 b
& z/ ^1 j; }( \- t7 R, f【注:阿列夫级无穷大是对集合中元素个数的评估,如果按照某种一一映射规则把集合元素按有序集排列,当最大元素映射值不超过阿列夫2 时,则集合元素个数不超过阿列夫2 。量子态空间可以考虑把系统能量(哈密顿算子)作为排序映射规则,此时坐标表象中最大排序元素映射值不可能超过阿列夫2 】( n5 t% T' L! T, P( O
7 c1 ~+ j0 y% K, }2 h$ u' t {/ c" _" q5 i% {
(步骤八)! z3 I$ h. F4 ^) y
根据步骤六和步骤七,因为空间维度不大于空间元素个数。
! S4 K/ V) ~8 S所以, 完备的exp(ipr)函数集合空间的维度为阿列夫2: w6 y. b2 w8 V
3 y( G* o2 n. g5 r2 l! Y) J6 D
! a9 D* U8 h* [0 L" ~3 R. |' K. U$ `- _4 M8 e6 G, M$ _% V% s
证毕。】
2 J& M& n! H! v
, l0 ~1 J$ f- Z5 ?
1 l3 |! q: L$ ~# P0 b5 ]( I N$ ?2 s! O
7 M* y/ w+ h, p* O' ?
! {* [/ N1 C" B: c- s# N( a3 Y0 b {" A
4 \8 k5 Q0 x2 f: N. U0 }5 f
/ F* M6 O7 l! t9 U* X/ e) M6 u; j. U4 {1 h+ I4 y
) z; R6 [) _, C
# g% B. M7 l$ d7 B/ w
(上述证明也许仍然不够严谨,但是在和李铭老师不厌其烦的讨论中,比最初的那个粗制滥造描述要强很多了,在此感谢李铭老师,并期盼其他朋友一针见血的质疑。), O& G, I. @- u( X9 Z
3 x8 u. C' X' K+ ]' C: T5 W+ X
" ?7 t# O0 l3 f4 W' X4 }0 W" b' C7 k. M3 ^8 f. Q
一直以来康托尔“连续统假设”没有得到广泛的认可,所以,以其它理论来证实“连续统假设”的正确性,是本文的关键论题之一
7 v0 a- N- w7 U8 c3 l; i 1、‘不完备性定理’的证明和‘连续统假设’的关于有理数和无理数的论断是等价的,这说明阿列夫0级无穷大和阿列夫1级无穷的逻辑存在性,说明‘连续统假设’有意义;
# V2 v1 ~/ T9 U* M 2、根据‘不确定性原理’的“‘完备的共同本证函数系’和‘对易’互为矛盾”,当我们发现‘存在exp(ipr)共同本证函数系’时,即证明了其共同本证基的不完备性。注意,这个证明过程中不需要引入康托尔‘连续统假设’。6 W# T5 K) |* i
3、当我们进一步观察exp(ipr)的空间维度时,才发现完备的e^ipr即‘e的实数势次方’,根据‘连续统假设’得知‘e的实数势次方’是一个阿列夫2空间,而这恰好可以解释态空间的不确定性(不完备性)。也就是说,要解释‘不确定性原理’需要承认‘连续统假设’的正确性。
# [4 i" Q0 B/ \, p+ j+ H) w- o
7 h; E, y. G0 w! V% s[p=25, null, left]么“不确定性原理”、“不完备性定理”、“康托尔连续统理论”,三者是自洽的!!!
6 F, P: v# c0 M" K. o; W7 t) e- Z1 v7 e3 P; h3 x
 8 _) F: U6 J! ~3 v. J; w 8 _) F: U6 J! ~3 v. J; w
! l# l5 _( d v' ^) T
0 W4 G- c: _" _. ]8 U7 K# @ 如何看待不确定性原理,以高斯函数为例,高斯函数原函数与其傅里叶变换函数之所以体现不确定性关系,表明具体的两个对偶高斯函数的本证态exp(ipr)并不绝对稠密,换句话说具体的两个对偶高斯函数的本证态exp(ipr)之间有‘空洞’。 因为两个对偶高斯函数的基矢波合计只有阿列夫1那么多,远远少于阿列夫2,基矢量不足够必然存在不完备性,所以高斯函数原函数与其傅里叶变换函数体现不确定性关系。
9 k) e/ [) I7 e. o% G 做一个类比,我们知道,完备的‘2的阿列夫0次方’等于阿列夫1,当阿列夫1的空间上所有数据‘稠密’时,即为实数连续空间。但在离散取数时,‘2的n次方’分别取值为2、4、8、16、32、64....,显而易见这些数字之间有‘空洞’,非稠密,所以其离散状态对连续状态是不完备的。, S' G1 ?8 A7 w8 X
1 o4 V+ d. b, _" l 上面的现象可以概述为:4 @- c: S+ o. v: ~: \& t/ N9 b
1、不完备性定理说明,阿列夫0级别的基对于阿列夫1维度空间不完备;! U* p) k, b) ]: i0 l
2、不确定性原理说明,阿列夫1级别的基对于阿列夫2维度空间不完备。* \2 w+ s) T1 e, l: V4 j" c
- Y( O, T" l' k; F, x& s: k
$ i0 f1 P. \0 u4 X6 R 进一步看,所谓平面波exp(ipr),并不是指一个波,而是一群波。这一大群波,有的快有的慢(频域)、有的长有的短(空域),在量子态空间中所有的基矢波总计共有阿列夫2无穷大之多。阿列夫2之多的exp(ipr)都是相互正交的,它们共同组成了一个阿列夫2维度的线性空间,表征完备的量子态空间。
5 H4 o A" Z G' a1 B$ r) ~ 基于此,可以判断完备量子态空间本证态有阿列夫2之多,其投影本征值x也具有阿列夫2 之多。
! P2 {6 P: q7 t: n7 V$ j6 D( @ 所以阿列夫2级别的坐标本征值x远远大于阿列夫1级别的粒子实际坐标点{x},因此阿列夫2级别的量子态坐标本征值x在阿列夫1级别的三维现实空间实际坐标点{x}的测量中表达出随机性。所以说波函数不是现实实体波,而是逻辑概率波。; E: @" c5 O( h* `7 P8 U1 Q. R
4 x& Q3 v) f3 D5 |+ h& T
8 S, y& y, n% ^" Z
) A1 @4 G# w& d9 n5 k3 e% [

7 \/ v" P; A7 e9 G, X) _# B7 k) t3 V) \7 o2 R
- O: k( ^2 n w" o. z 咦,‘阿列夫2‘维度空间?
- T( ~) F8 R ]. `' v: v
1 Q" i) ^- t# g. R+ j$ A; x8 l; A 没听说过,真有阿列夫2维度空间吗?阿列夫2维度空间有什么特别的地方吗?0 {. M# u; L1 Z; K$ C2 S/ ~& o
5 \) ~( a+ D2 I2 X X1 v6 a" @5 V' H
《庄子.天下篇》:“一尺之捶,日取其半,万世不竭。”以这种一刀一刀砍出来小段棍子,其实就是一个有理数的数列,是一列有理数,而有理数是可列可数的,有理数的全体构成了一种无穷大,即‘阿列夫0’! s! Z2 c, s' j% u T5 P% y
, H% o7 h, @1 j
微积分把无穷大的级别由阿列夫0版升级到阿列夫1版。人类的视野从此也到了一个崭新高度,达到前所未有的广阔空间。
/ {% L) Z; V; M! \
, g# _* D' U$ a) a2 G7 w 量子矩阵力学,通过傅立叶变换对量子态的分析、通过不确定原理、通过概率量化,把无穷大的级别由阿列夫1版升级到阿列夫2版。' ^: A( {1 C; W) c2 k9 ~* I
5 {* O* W+ |3 I P# ~1 ]; W! W' E
" J/ O$ i4 o, \ 我们已经知道,阿列夫0是无穷大家族中最小的一个。虽然同是无穷大,但阿列夫0比阿列夫1小得多,到底小到什么程度呢?. ~# d) e4 m. J7 f
康托尔老师告诉我们,哪怕取很小很小的一小段连续实数中的无理数(比如从0到0.0000000000000000000000000000000...........1中那么一丁点儿小段),也比所有的有理数全体(即‘阿列夫0’)大得多得多。3 W( Q, P- J/ y- q3 U
同理,那怕‘阿里夫2’空间中一丁点儿线片段包含的数,也比整个连续实数点的全体要大很多很多很多。
0 T r* e0 u- C, {, C5 {- M E8 ^. Y) w 也正是因为阿列夫2级别的无穷大的广阔巨大,所以对于任意实际的物理量,我们不可能既在时域看见它处于粒子状态,同时又在频域看见它处于粒子状态。因为若如此,量子态空间就不可能大至阿列夫2级别的无穷大。(三维空间的粒子数量充其量只能达到阿列夫1级无穷大,但是波函数函数全体却可能多至阿列夫2级无穷大。)+ W Z! w6 E' F
( g2 c9 P' U# d( @
& r. x. q' `2 V
! V# j- G6 z" `5 P1 ?6 B# w 人类认知的足迹,是从眼界的拓展开始的。最初原始人局限于所在的部落领域、后来扩大到呢国家、然后环球旅行、逐渐了解到到广阔太阳系、再后面发现了更加广阔的银河系、在望远镜里发现可见的巨大宇宙、又推断出红移后不看见的更加更加巨大的未知宇宙。4 F- _# B Z4 W& X3 {' [
( R% ]! ^" Z( k. u5 ^# q) z
现在,我们终于发现了一个活生生的“阿列夫2”空间,这意味着一个更广阔的宇宙,比大家熟悉的实数连续空间更加广阔得太多太多。无容置疑,“阿列夫2”空间的探索必将带领人类迈向新高度。最初,我们计算从一个点到另一个点的逻辑;继而,推演一群点到一群点的逻辑;再然后,分析一个点集合到另一个点集合的逻辑;现在,当我们考虑一个子系统群到另一个子系统群的逻辑时,那便是迈入阿列夫2的领域了,这个领域是如此巨大广阔。' L3 Z# y4 X' d) t$ a6 T0 b7 ~
& p( L# d1 ]/ Y6 P4 f) P, h
* ]9 `" W3 B" ]/ V 如果理解了‘阿里夫2’,就能理解到神奇的exp(ipr)基矢量空间的广泛性。
: A% A/ S& @. n u
# @! e( x# F5 F6 w2 m4 `( C+ e. O 从古希腊、古印度开始,人类关于物质是由不可分的原子构成的概念流传了上千年。但是,近现代以后我们知道,物质虽然由原子组成,但原子并不是不可再分的,它其实由质子、中子、电子组成,还有费米子、玻色子,夸克,其它标准模型的基本粒子等等等等。光这些诸如此类基本粒子概念就足以把人吓趴下,晕你个半宿。其实,简单点,若果有人再问到基本粒子的问题,你完全可以回答,它是exp(ipr), 因为exp(ipr)是任意线性时不变系统基矢量,这完全可以看作我们所知的一切可测物质的最基本的本质粒子(当然这个叫法不太严谨)。" X0 ]4 _0 d- e" \
/ d8 z4 f- n- \! [3 c
i; j8 p$ T5 t
再举一个例子,在商品社会,钞票是所有商品的度量物,商品的价值的体现要看它值多少钱,值多少元多少角多少分。“exp(ipr) 是任意线性时不变系统L的本征函数”告诉我们exp(ipr) 本征函数的通用性,本征函数就是坐标系的度量物,形象比喻,exp(ipr)就好像是线性时不变系统的通用钞票、是所有可以度量的可以验证系统的硬通货、是全体自然科学分支的统一度量衡。
/ u K: }; _% @) _
) b2 d/ ] [5 Y3 t! E; z/ N; h: d$ Y& w7 f# s# E$ F
这个神奇exp(ipr)宝贝精灵古怪,不但玩遍世界大小通吃,遇魔杀魔遇佛拜佛,是天上地下前门后门的硬通货;而且还能玩穿越,穿越时空,同时穿越时域和频域。这个异度空间的幽灵到底会为我们带来什么样的独特魔法呢?
" e( P4 o( y2 x; O/ [3 T) f( {4 Z0 M3 L5 Y5 i. Z! ^- O
( e4 P, y+ f# J" e
4 f( g( n% k; [$ V2 @( W$ k
7 i& t* C% z6 m x! a4 }2 Z |