|
  
- 积分
- 13286
- 威望
- 13286
- 包包
- 34831






|
7.3 多重线性关系
# ^$ m, U( R% v) N/ U0 N3 w4 c" d% `1 |& o o4 X0 a
4 d% n4 f+ O q
, B2 _; X1 _: n( ]2 j
4 y' Z$ f* F8 x) C
; \, j0 ^" F$ }5 u; K, k. o0 E3 C3 F- H; T" d2 w
# W' w0 }! [/ N
1 X8 e! M5 m8 s0 T, g3 y; G5 a: y9 g0 a
) f; l( S1 }/ Q+ I7 U* Z
未来的某一天机器人会不会替代人类成为文明的主人?% h% M+ \# g+ `: G: G
+ [) y" }1 G [- A
$ i2 R6 y7 b# n6 S H 由于人类知识水平的局限,我们即无法证明其真、亦无法证明其为假。
6 l6 ~# m7 F1 o4 O
! o# v- l9 u3 @) D3 H8 \4 }$ q6 l% \9 c- w
这其实是一个人类认知所无法判定真伪的“不可判定命题”。$ b* w, V, L5 L+ J0 ]
% D/ K8 {6 o+ `' l! t0 Q1 [" w
: l# `6 u. g6 Z2 V 也许,关于计算机代替人类的话题,目前还只是骇人听闻的哗众取宠的龙门阵。
' e, y( t! X0 Z
8 G4 o- W( x$ y6 j& H3 G" k
. {, D' H5 d6 a4 t" {* O% h9 m4 `2 n! @0 e
: B3 e8 O& _% r# ^( ?. A$ f
' M1 K$ W8 T: f$ ^6 H( H, ?
) O# K) C4 I4 l( f/ b4 `
但是,我们可以确信断定的是,“智能爆炸”的时代正在到来,人机共生系统在可见的未来将会得到极大发展。人类的生活将会越来越依赖机器,甚至如果离开计算机的推演辅助,人类的思维很难从一阶逻辑向高阶逻辑突围。
. I3 A3 D7 n5 z4 D! j7 R' X; u8 H$ F0 S# x5 C1 N1 r0 G" p8 X" R
' d% \7 r* e g J) P# n 在普通人看来异常复杂的高阶张量,用计算机演算却非常简单,只需定义不同的数组类型,然后将对将、兵对兵、钉对钉、卯对卯,对应代数运算即可。, b" r0 g6 h, l6 G4 [
9 {5 l$ `5 c6 Z% a/ U! E* g
: g9 R! Z6 `/ x) D. [ 比较打击人类自信心的是,以张量语言而成的相对论对于绝大多数普通人完全就是天书,因为普通民众很难理解其中张量的内涵。那么,通过能够轻而易举演算张量的量子计算机的辅助,人类可以“理解”到其中的高阶逻辑含义吗?人机共生系统可能因而变得超级智慧吗??( X6 O6 G! ^6 M6 V$ G: Z3 h
- F3 k# i, e; l- k/ |* ~0 Y0 F0 ^3 E- R% M& x
2 }$ T/ l" l$ k9 Y( U- ]
0 h: N; E, ]: E8 z2 Q% H+ m( v& v: D" J# N: X1 n
3 n/ E+ J6 c$ E) B$ P" \! z, k: L# M
, n o8 O% Q7 ^. k8 |
) b! p; w+ Y3 u2 G. M2 Q
' e1 Y" o6 N1 v/ `. [: r 基于无穷维张量的量子计算机到底有多么强大,可以从其无穷维‘多重线性关系’一窥究竟。
* |! ]2 I, \: c( ~% a- m& }+ @) F- P' v% x* C
2 N" w5 \2 ]8 o( U
! u; Q. d" J- J) G9 O" R/ e/ t5 v5 c' `
# R$ o& j7 x) w* P
) e5 M4 m: c# b1 A* U1 i; L5 Q9 z/ }
/ a) Z6 b9 H& n: g9 _( B
5 M# S i# f1 Y Y
; T% E9 u4 A' J
先从一阶张量(即‘向量’)说起,向量是向量空间的元素,向量空间即‘线性空间’,满足下面两个基本数学式子:
& y. B4 M6 ^+ g/ I, S
7 z: x$ F' Y/ v3 P4 g+ n
; y) R; |8 |- M. N' i4 w/ Fφ(x+y) =φ(x)+φ(y)) {2 m1 k/ x! o) S" C
Z# I' r3 G* I# n A) X! ]# Q, {* G& s5 `6 u2 G! C7 O3 R% F P
φ(ax)=aφ(x)
z9 K$ \- n1 r: W- I' n3 [8 a, j6 \- k, b" |
( z1 I* B: j U* u# z( I1 L' ] 形象理解,x、y相当于元素“种类”,φ是某种“属性”。当一种属性作用到一些种类时,如果满足‘叠加原理’(也就是上面那两个数学式),那么具备这个属性的空间就是线性空间(或者叫向量空间)。+ N S; A! H- P9 Q
( {; w9 a# D5 t6 r% c" C" @/ L! r$ T0 i4 O
' O) @" {8 Q: P( n; [
8 y& b( s( F6 p8 K0 k% K
9 ~' z" F" y3 {" f1 J* G0 n
$ e3 a- D" @5 X7 t6 q8 e0 o. y5 x }# q8 m
" x! c$ b! B( N! u3 D
) c2 {( D( X& C9 Z! q
5 U9 l) r7 ?3 w# \* f" [' x( \" |' p" n0 G4 b- Y1 I$ T
& E, a. O0 s6 [
: x9 r7 L0 @! L/ o
' Z7 X) R) f! P$ F9 C# [
w- j/ w" a/ K1 _5 ]0 Z
! c/ f, J3 P6 r5 k5 `# L- e6 I. @# @
1 W1 q4 Q' X( o+ ^8 i1 R
- X* d2 X9 ^' Y9 x: v \# j1 X+ z3 ]: [3 c+ ] ~2 n' E# s
* }6 o7 y8 }; f I6 C$ x* \. L+ ^; a( @3 N" ~5 Y8 D
- }0 p# E7 ^/ C2 K2 x
5 M7 ]2 X. j5 ^8 D+ r ]
& f3 y: {$ s' P9 N) j+ M" M
8 n* |8 Q, s; @+ x' m/ k 向量空间的元素“种类”可以很多,但其“属性”是单一的。如果我们对向量的“属性”进行扩展,比如具备了φ、ψ两种属性,满足:
2 d8 w7 U& K5 o4 q
. x7 A0 a7 c, ^9 t) K
- H2 }7 p \8 S3 |$ M(φ+ψ)(x) =φ(x)+ψ(x)
Y. o6 U6 z8 w6 b1 w; f/ @; a
* t$ J6 b1 b. ^, A' `* _, o4 A
4 h5 l! w% y6 U" t: n7 s+ `(aφ)(x)=aφ(x)8 M+ e* O5 D# f' o S
3 C' O5 o5 e7 J
( U9 }. D% N* e ~- v
那么,单一“属性”的向量就从一阶张量,变成了二阶张量。数学表达如下(为书写方便,定义b1、 b2 为属性,a1 、a2为元素种类):* u1 ?& w: b' Z: U+ `6 _
) t# f8 k) w% [4 m0 [5 W7 N! ]4 X1 b. Y; g
) [( p# ]# S$ {" E
' v8 k8 \: @6 D1 R- |
' N6 e) m3 R9 k: _ L" k

/ L% l: v0 D# J5 f. o4 P0 }5 g0 v5 N ~' ~9 q% y2 @
6 ?( K. e( q( y
$ a9 s8 a, Z1 M1 G/ d" I. A f: o3 U+ T* d" m
0 p. C& a2 ]4 G5 C, F1 J/ ~
s5 {$ ^/ C; l
|( x1 X4 ^0 f" {1 ~
" h2 v# g- ~: P% k, }: |: ?/ B
& ~- T3 V8 Q, F0 T7 v! y8 C$ t
# }1 Y) }" [2 V# Y# e: M
1 i0 I: o8 Q6 ~: \1 q
9 a7 K, ~& m4 T, h1 r: V 更复杂一点,可以定义m×n维的张量:
; o9 j2 U9 ~8 m& r) L2 O, z/ h
- T! [9 a2 R- v5 L5 }/ f* q# U" P; l {( z3 d! @
, }7 f0 z9 y9 y& e7 S
8 k; i9 V5 H" l3 o0 n
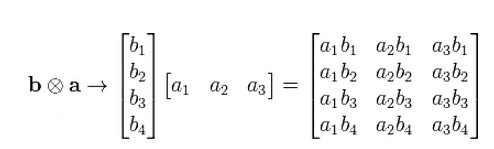
# ?( k- ] z' j; e1 ]9 z- c3 ^% l- `3 s, f4 B; d1 v! u# p
4 T r; V0 o W/ M; h: c- [8 x: d: o: r) b
* M& `% v' i' a5 M
# |/ h/ z7 N" F, K! [5 g" j% e) f+ E" x
' e: x2 |7 {8 `- P5 } C& {# r
6 p! n q& M1 z0 V3 f3 K; t
) w4 i, [* S1 G( e# p; |/ K
5 j' r& u7 I- N* x3 d
) H0 o7 v# p1 R# X# m. I4 V) J3 R7 S9 b# @
- k+ U% C+ q7 @( Y3 s: t
注意,上面两个例子都是矩阵形式,即二阶张量。张量并不仅限于二阶,还可以扩张成为三阶,象立方体的样子:
8 }; Y( e; }5 ]# I: }* u: T9 H. |9 F8 ]- Z+ w$ T& o" |
7 \$ ^1 O, b& P$ b9 R
# @ C& G, l- K. n; K: O
( {. W5 C" x8 P9 a8 c% y
3 A" F0 t2 r+ G7 H
4 Z) c% w$ K' Y/ j2 [+ U: L! Z# l! H! ^7 ^& T1 y0 m( y& @5 G
' Y$ c7 s; j* J6 o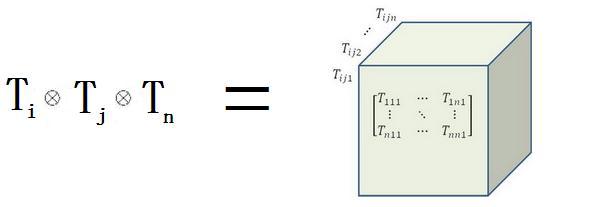
7 a5 a7 w# r F& D: {- [2 n- k m' v/ x" ^ W. g& M4 w* ]
& l5 T1 X/ d2 T9 m# G# K
" } O* M- o) `8 w7 o" [1 r3 `" r4 p! y
9 a( I7 D6 G" r2 m0 G) s: @5 A
% r0 b* }% q. l- R7 ~& \! r0 Y2 \" a, M8 j( J& ^0 X
: `2 |0 K4 l4 J+ X+ S
+ B! e( E" R1 ? 并且,还可以继续张量积到四阶、五阶......无穷阶! A% `; K& a' O/ |2 d, _) J9 ?6 u
8 N; }. v2 p. ~+ x3 s7 G( ^2 [
4 \; v* T4 _0 E
(更高阶的张量画不出来,嘿嘿,只有自己想了 )! o6 ?, P# g3 i% J
* B1 c' M4 v1 f8 h1 f6 t( V% N* p. e- s; B' T$ g2 u* z' E" s
t, v; G) h. V. `
9 B) p: A/ u$ r: s2 e
% f/ v4 s# I' c9 m$ y& y) S
% c0 u- k- n: b- h- H7 n$ i9 S7 k 形象来说,张量就是“高阶向量”、“超级向量”、“广义向量”。因为向量只包含单一性质属性,而张量包含了更多角度更多属性。- V2 v. V4 W/ Y& k& S
7 E, X0 y! O! M& t5 b
6 f" U1 T2 Y' g* K3 r) q
9 w6 n9 y& K8 t: ?. [3 H% I; `4 K' H% R
, b3 I! T% ~7 Z% z4 E! S* t' n/ P! h, m0 v5 F9 V2 w0 O
# E5 M* [& @ ^" [) Y2 x1 C! |
6 [. e( _' [. i3 k% y, z Q6 m
' y' v3 Y# y+ Q: z/ @6 v; `; f& c" t7 H2 E1 m
" U/ Y# r$ ?3 A
+ e5 q* _+ D4 l" ^6 p: B; f# s
+ u2 b4 o% v; {) k8 B8 o
( Z( p6 k, _, U' G. X* T. @; I+ K- I7 w+ ? j$ ^
( \; ~1 V3 R3 Q: `
( B$ s: t8 ~; A
+ @' S. z+ D/ A# d- j/ \0 R/ k) w& k4 i5 I2 }
1 x4 p* J f/ L+ K! V7 o: x* h) b$ N# W. Y7 b& h
. T# S" N [. N0 a6 r
8 w/ k7 }, l! f0 t7 p8 s( `/ k7 m' q- C* E5 L# F4 `' A, [9 M( S! R
+ j% S% n) K' Q* M1 [# D' I( }; g+ f) Y. F& l; q' U# e! {
F& j2 Y% u( M0 @8 X. t* G9 m3 M- t
! t6 I8 B" |: N3 M
$ i- J2 U) l0 B5 D) X' s
4 G& H2 L6 |9 U- x6 k C
( S% D L( G6 `* ~7 @: {# Y% i
- K6 D3 B4 ?. F m7 E' M/ f3 S2 }: \( G- {4 q
2 s5 [* @/ P) [) u8 J4 x7 [
9 P n8 U, M; h* k( h4 y" _7 n0 N6 }1 o
) b6 U Z; @0 D+ I- h
对于初学者来讲,很容易混淆向量和张量的概念,特别是在有限维的情况下。再来看看张量的数学定义式:6 m0 s0 M7 b' ?8 j
6 U3 |1 B# _& Q
) P7 _9 @' j a. C(φ+ψ)(x) =φ(x)+ψ(x)7 e; o K/ m4 i5 g5 U
0 j& l3 }) M% ~$ T
( v" a- d1 U- F; w: f( U% P. v3 u
(aφ)(x)=aφ(x)
# v% |% x. g6 q" Q- R
9 G* j# a9 @" v" }& l% X/ k$ Y; a+ t9 i8 M
上面两个式子,很容易化成下面的一个式子:
& U& v" d% }7 b5 w. s4 r. h, X! j# Y! z/ n N
. J$ K* A: K7 N
(φ+ψ)(ax+by) =aφ(x)+aψ(x)+bφ(y)+bψ(y)5 v( |- {* h0 Q- S
6 c- i4 x/ h Q$ B& |( a8 Y2 ]( X, d8 F/ \5 U1 [0 C1 H
咦,如果把φ(x)、ψ(x)、φ(y)、ψ(y)各看成基矢量,这不就是一个向量空间吗?2 R- b( i) O# a' ^
8 F- t5 X; K9 a: c! z& e
% |& t: W. U0 X' Q. f. _! R
乍看起来很像,其实不然,因为张量空间中的 φ与x、ψ与x、φ与y、ψ与y 还存在单一属性的向量所不具备的更深层次的复杂“关系”。
3 y* b$ l# v5 r9 s
6 g7 I' M7 L' v5 P4 S1 J$ N5 `% q. h5 e- S! s
& n. z0 B/ Q3 s# K. h) M1 } m9 Q
" w7 y( ~9 L4 m! Z& V; R \% G) u5 R, R& v+ G* e! W
, h+ z# ?/ M% C6 b5 p
5 e4 |* d0 S* t. O/ S
$ u6 u+ i$ C& m: g, H+ I5 ]; M6 O
$ ~: u( R5 F6 o& n, T- i* M5 c( w! A. X1 e6 [9 `6 y
& S6 @3 s& _- b8 U3 e, M+ M( s- z& r* n
$ ^. ]9 L& I3 [* \' M$ T% D
% M- `% J+ k2 }
* [* H+ X' P$ b- p( g S
1 K: E6 B& k0 y! [5 j# [) q M2 K5 r* n/ x
8 r9 [- R: H( u( `5 v% i5 ?# i: b
7 j* `- e1 |' u- I+ s' a
& h8 v) X2 K+ s5 U( T
4 o% q8 |) c l6 [/ S% I" I. }0 I
7 r: E2 q2 M+ e* l0 C9 r( h8 Z6 C ~' ` B9 ^4 ~1 J P
- @" `- }; f) c8 S1 {7 n6 G3 t
& `# r, N/ a7 l* J& _: M e% l- [3 v; I9 `' t( V$ _$ y
关于“属性”和“种类”的这种深层次的复杂关系的量化,数学上称为“对偶空间”,式子如下:9 n. t! H" K2 x% X: h7 u
6 M5 Q4 @* ~. M
. v/ B+ I% h7 K% X* b* \* b1 J) G(φ+ψ)(x) =φ(x)+ψ(x)3 ^8 ]+ K' @; ^. N+ z+ Y
* K% p- Z9 J" I: f# D# ]- [7 y& w- |+ k8 b. c( d7 K' H
(aφ)(x)=aφ(x)3 o! h2 Q/ K1 O+ J
( V9 y2 y; z) e L- w
8 p. z; U) g! b* t0 E- {! Q. F 其中,任意φ、ψ∈ V* , 任意a、b∈F, 任意x、y∈V6 U/ i! {3 j6 q- Q! L9 A% ^' M2 }3 a
2 \5 g) I/ R& n
( W2 w7 M. ?3 ~( o6 v! w; J* O4 b
. |: U V6 X9 A5 g/ H/ U0 s
) T: ]3 D# O; f4 k9 z
1 y7 n6 f6 f' y% \" g4 s+ F) W
. p X8 d) p3 a% ^- {2 v \ u3 O 请注意上面‘任意’二字,这意味着“种类”可以有无穷多个,“属性”也可以有无穷多个 c+ g4 n; E8 X
1 Q. x& L/ v2 K2 E: P+ W/ p, O2 e( k
/ z' X* h9 o8 w& f 为了表达方便,称x、y所属的V空间为原空间,则φ、ψ所属的 V*空间为原空间的对偶空间。二者单独而言都是线性空间,合计的张量空间满足‘多重线性关系’,具备多重线性映射、多重线性属性。
1 B/ s8 P$ g" U* r- O2 }: Q2 h k# C4 F
. ?5 R/ B% d- q1 ]0 b8 U9 i
C5 A" s! t4 h7 A2 E' w
8 G; U+ K2 _' }# d" }/ b& c( z4 r' l! A w1 b
* Y2 \' ^- j p* P
8 Q$ G3 V; ?4 _3 i3 A8 l$ n8 ~8 d, l
3 M5 h. h1 o" Z) B! \) R0 {
1 w2 p$ }4 i, U: C" `4 }5 ^7 J' }) S. Y" p; A* t4 q" ^3 v
, T: n+ E6 O- U, ~
u" R: c N+ c# a) m! E
3 D/ s1 y. D- D6 `3 O1 M# s8 A! E8 U" Q8 Q; r
. h6 M5 ?$ t2 k
! t+ g( f) D1 c
" Q+ Y! N* f- Z" ~/ h' h i+ |- t% i- l
; h7 k* u9 [% Y1 ?2 |6 R& e6 Y
; ], ? X+ ~: P, U/ t/ F9 _6 j5 H/ U- B& q- w
! ]; c8 d& b9 J+ p! i: C
( d p' S9 Z8 p/ p
$ m6 X5 T1 F5 a5 ?( f+ O
5 ~9 e! _) I6 [- q
, d* f2 L9 c$ E: V" v) i! m1 S7 `2 Q" Q
$ t" d" ^; P9 B6 u2 n& J) t4 J% C" V! b" @
2 ^! Y: }3 j% B7 _2 [' N- g' T6 C
" v3 R! t( ^2 R! m; N% |
& D# q( A3 z h; e4 X# f6 H
: C$ X7 c8 L1 ?; v& y" n5 u$ g% H! S! r4 T) ~
. y/ j/ `* i( q9 X7 d5 T7 s; `/ [# s& d$ I
# h8 l7 n7 B$ B9 T; F* q
/ J8 Q* ]# k f6 l
- S% P$ w( Y' w5 B; b" |) |9 w9 l' L! ?6 B b4 H" _
& d# ^2 v: L3 h/ t
' ` E$ v0 a/ m1 Z
2 v) q6 U; x8 h# O7 Q L! X/ {4 H
* j% M, p) h! U, v2 N! V, J0 i3 n5 c- w1 m
! s, |1 o9 b' ^( X. h- x- j# K" O% m
: _) ^3 n) e$ M2 y( ?$ }. ~1 n8 |
9 ^5 R4 `, G# ~! e8 d/ X. ~
; C/ Z0 K( U) B4 G/ ]* K$ G/ E% F- U1 H7 Q/ }0 W7 I
2 ~: C `4 J" ~9 M3 M: `
) v0 M: G/ X# C( r) C
; p, t' u2 D$ h7 B" k( ?( k7 _8 U
比如,你买了一篮子水果,水果“种类”包含苹果、梨子、桃子、西瓜、荔枝......
% `4 B! X& t- F% `
3 {* n% q. a7 K% R! a2 l) T3 S" @2 |7 @& i
7 E# Z2 l0 X5 z
7 f6 m1 a+ G2 n m
' h* g7 |9 ?0 Z
1 [! d6 _5 i' |, T! G R( @6 [" G( Q
/ Y D9 Q: ]% @# _3 x# K
4 r7 ~+ r- w6 y9 N
# o3 g" {# }" {7 Y
, ~, J$ g z$ d q: @2 P) ~/ g
* W- D7 q+ e! R9 C/ g& A
$ O/ `) t; s- `0 n% ?5 [
( X/ C& a1 g! i- C4 M6 p5 q
0 v. R# H$ Z, F9 N: h* a- {$ h A
+ j& P+ B" T0 K: n" N) h" Y5 z7 K( T7 \7 N
! [. o, D/ o$ o Q1 c" t. \
5 U8 B, ?) ?* R8 ], u+ r8 C 其中,苹果分为红苹果、绿苹果、半红半绿苹果......9 T) u' `, }% i5 ~+ H* p
" k, N* ]* ~2 y' }: @, h2 Y" @
3 W/ b$ D0 @4 O; m! Z8 j. I
其中,红苹果又包含大苹果、小苹果......4 u y3 S" D' U8 z& M# L
: ~, u2 r* Y% f; L r+ \' H' c. y
, i" y6 d5 |8 e- U
其中,大苹果中有些是新鲜苹果、有些是不新鲜苹果......
2 m U+ ?+ P# a# @5 X. H/ y
' p$ f# o4 h# R# @! i4 F2 ]0 k
其中,新鲜苹果又分为南方苹果、北方苹果、美国苹果、泰国苹果......
- F; G3 X$ O) D7 ]! e, q$ \
& V! r/ J+ w# |8 U: r0 `9 {! j: W5 y( f: ^' i. N. E+ i; n
其中,南方苹果又有甜苹果、酸苹果......, |" g1 O: P0 [$ l0 ]) G
* t% d$ n' E! w7 a% b
2 u6 _- A# O) {# x4 O C& p0 u" [" F$ k8 S! @9 t2 d% M( d: h
! a% W5 c4 x$ d* D7 `" j* B9 Q$ K7 r
2 h D2 l" x2 @# C) I
这样的属性细分,是可以无限细分的 O2 `6 v) S) |; o4 O6 l
# v3 p8 I8 f1 I5 G- G4 X$ o% W# g
z1 C2 c7 K5 q4 x9 V) }4 c
* X- t* ]/ _& R8 `* Q6 Q" e+ N! A- t" D
" L) n8 U4 F' t% k5 [$ x$ _' @0 x- |
/ T' F% @( S A' H+ q" j ..............( D; ]! v6 H, E4 m/ ^
- g0 F; Q5 N. n, R5 j4 e
; v% c$ z' s: Z( [# @2 E5 Y* c- j; v4 H/ D3 X; [" W5 [
* p' x1 [2 B' z: z' {# L$ ^' ^
: Z" g- e, t, w$ P- |% R3 A7 x
! r9 P& w; J+ o" F
$ z' ?- |3 x" ]: X! a, g* J
7 Z& O( m7 P+ n: \( e
7 K& s; g2 d- I' }& P- b' x1 T" Y8 C+ G2 M& N6 n
7 c. h' T8 Z4 a
, H6 J! D" s$ w O ?) P
5 d$ T- V0 Z. |7 W; i! f0 B; p2 w/ o3 U; V; n
其中,梨子分为红梨子、绿梨子、半红半绿梨子......* r" D! q' w: ` F& ~
: \% M1 E4 B v/ c2 e9 C6 c' I/ f
其中,红梨子又包含大梨子、小梨子......3 F% a$ ~# f/ }) \3 D/ s1 U
- e. T5 K2 u4 ~7 N- B6 V
4 S9 T% i$ T* z: y4 ?$ ~7 Q$ o$ y; M
其中,大梨子中有些是新鲜梨子、有些是不新鲜梨子......
, \( J+ }$ Q7 i
9 r, b+ h4 g! M% g3 x
% Y& j3 x( F( u. x7 B" e. J( H b+ H 其中,新鲜梨子又分为南方梨子、北方梨子、美国梨子、泰国梨子......
7 p- ?& v" p7 c& q6 K P
+ c. n) t! w. H- j, ]) O7 O8 v+ \4 ]( a+ p
其中,南方梨子又有甜梨子、酸梨子......; C# C$ d* p- ~& j
9 u$ c, ~0 x$ J: B
n" X* s+ x! C0 `
: I" W& n, L9 e1 j" d- L6 D
- j( `1 ]2 D0 J8 \- o
; \4 [( E' s( s4 ?3 u( K0 ] y) e" o0 @! A, s; Y" U- i* G
这样的属性细分,是可以无限细分的! i# T) W6 m' h+ b+ d U
8 L3 P. V0 B* c' p
4 |- s, W1 N( L: z# F' D' k& _$ J2 R: n/ ^7 C( T1 }" b
) j' u$ t* B! n: d
6 f: A: f; b+ C) q: P. n* ~0 z- {4 L7 u! S: m9 z3 Z
..............
' E/ s& L7 x. I/ x7 g4 H; q O2 u- v4 B5 p ]5 P
' }3 c0 |* `$ g0 j; a$ h& C! d$ K
% y% B$ X. S, O, z1 Q1 @5 V+ A' ~" B e
! q3 i! u7 S4 j- p" F; B5 i
7 u0 h* a( n# J& n% R- k6 Z0 E" W
- T6 p' K/ Y" V. P$ n0 K
5 _: {( F" |% l/ R# U! r' j9 b5 h, N: m% E' J& U! l
' H# Z( }, f4 w7 V9 d
3 J6 d' `, K8 ~* Z
) W4 R' p: l* B5 e
& U8 q* @ F" w3 F( z( o 、、、、、、、、1 Y9 e8 R# F" T6 m' ~
% Y. v+ j- z+ ^0 ]4 E8 |
8 q- C5 a0 b( @* m6 u1 \6 v' p
0 ?" }4 j+ d' E( J: O- }- u) m0 a' d! |& o# q
3 D( r2 O2 z2 q! Q C
$ P5 A t" X1 {8 S9 X0 b0 J. J) |1 _/ i H& r# @1 d- F6 e$ t' Y
( u- T& D% E2 a' \( n" g3 G8 }5 ?
* R7 O6 J; i' O# c0 v% v$ ?% X4 K5 X D5 B) B$ K' f! b6 X1 |1 x( k9 S; f
+ _- `! O/ L# l' M6 H% W
, C5 R. O1 ^/ {7 |% [
! y/ h" c1 o$ ^6 C
; D8 P. l- S# O( @+ ~' ]
这样的种类细分,是可以无限细分的: D, }" W" O3 Y. ?0 h5 O
9 K& G' _2 x( W* \, p/ f: O9 m3 _7 t
4 g# |; p$ x3 w+ b) ~
. w8 j+ g( y1 H o- T( Z. v4 D5 S# D. J5 o9 G/ }! C8 j
& p# T! m) o5 e( e! b2 J
' H1 w/ ]% x9 V
: A1 O8 `4 \9 }+ @ K; v Y* ^3 _7 v0 s _2 D
7 ]( B5 e& ^) q. ~ 苹果、梨子、桃子、西瓜、荔枝.....等等水果的“种类”是原空间,
$ y# g) A' o* ^& R/ t8 _5 v0 k. g. o1 E2 J; }4 ~/ D2 a
( f% ~7 [; M$ S/ Y( m! b. `, |
颜色、大小、新鲜、产地、味道.....等等水果的“属性”是对偶空间。
( g: A4 \ _* L" k
+ {( c% k3 Y; l; ~) J o1 J- Z2 Z, _! D: U
: _" E$ a4 M' s+ d* f8 H7 h, O; \) r% ?: l5 u$ |
( c( o4 m& k% \, C/ @' J* J
+ d6 D9 ]7 ~3 ]( S# r 形象说,对偶空间即属性空间,以‘属性’本身作为元素。这些属性元素具备线性功能。7 A+ z5 N$ e, Y; m3 r6 f: C
9 ~9 d1 O8 }! E3 D0 l0 [
+ Z. k0 d( g4 ]: F% \& I( T: b0 h5 K" U' ^) U
8 v8 r5 K- y* |" {
* c/ S$ h7 j& x( _. `6 w+ }! f+ M+ Y `- P+ o/ S, p
进一步深挖这个问题,需要探讨对“属性”的结构度量。) v. N2 O4 x/ A2 A; \& W! A
6 H: {; s3 ^( @5 f/ | b
! _4 n9 a! {( | 我们知道,一阶逻辑与高阶逻辑的主要区别在于,它不允许量化“属性”,向量空间的“属性”只能是一个单一方向。但客观世界中,事物“属性”并不单一,可能包含了物体的多种品质特性。如何度量“属性”的复杂特性呢?. D1 A- z4 E/ B) T2 T) D& W+ @
+ ^/ `# M+ L2 r6 a8 {7 w0 U9 v$ w% `
在张量空间中,‘属性’还可以再扩张,比如把原本是“属性”集合中的“颜色”点概念扩张成一个子集合系统,把 ‘颜色’ 化为一个单独的子属性类。把其中的 ‘红色’ 、 ‘绿色’ 单列成为扩张成一个个子集合。比如 ‘红色’ 子集合中可以包含深红、浅红、粉红、暗红、朱红、猩红等等;如果想更精细,还可以在容许的红光波长范围770~622nm 连续取值。
+ Z8 \/ H2 o; ]) h- i/ G5 D3 x
* v2 t" o% V% A' C( t0 {+ Q L. M) a- t1 R: U
同时,“种类”也可以进一步扩张。比如,把‘苹果’点概念扩张成一个子集合系统,把 ‘苹果’ 化为一个单独的子种类。 子集合中可以包含红富士、嘎拉、桑萨、红将军、津轻、金冠、红星、红玉、乔纳金 、澳洲青苹等等苹果具体子类;如果想更精细,还可以包含‘苹果梨’等过渡品种。(‘苹果梨’是苹果和梨树木之间嫁接后产生的混合品种)
1 S7 H$ u* g( l+ O$ |- M5 I* j$ q4 [2 I$ R+ H9 U7 `8 N/ p
+ l0 i# z4 E/ T, R5 \! z, F
这样的m个‘子属性’和 n个‘子种类’构成的(m,n) 型张量的空间形式如下:& |# `$ R/ @3 @
+ v) l( b8 Q. a, n9 U
! Y, ^* e- @6 g
' h: {: |" ?1 Y' M
, Y( x% A9 z& w5 Z$ _
6 K, _! R' I- Z; J. e( `
% h! Q# g- q. d) q# M' U
$ a* }+ a* ]& T
7 Y" q0 J* ~% f. M+ V
% y+ `5 Y) C5 v3 E0 |) P% c5 F, v
) T; l$ t1 L4 W0 v7 {$ e
( s* r3 [ z; k) s) B- W- P k% ]5 n; i. ~* K6 E( l! ~

: B% m: a0 t1 B- Q5 S! ^, T* E3 V8 f0 R# o( {1 {7 U
# y1 G: c' y( B9 e% P+ O, t, x% Z) \, ^' R3 `
9 \, q, s' n& n$ c
$ P4 _! W/ u1 \1 u (m,n) 型的高阶张量比较复杂,下面以相对简单的三阶张量为例,形象看看一篮子水果的三阶张量表达式是什么样子的:
, U u" ^' [8 o6 k
4 }' N; J$ E8 h4 f1 h/ p
1 `6 t/ A: P& K; C2 ?6 v( C% c
6 c4 L0 T1 }7 r2 ~- b' j6 U" \& e4 l5 d) F& D8 u8 A
) B1 U8 Z. D' H/ k% l
) V$ X5 N$ \" S b( q+ {9 p( W% T( M( z; r/ r3 X
' J% s( \9 O, w) t+ M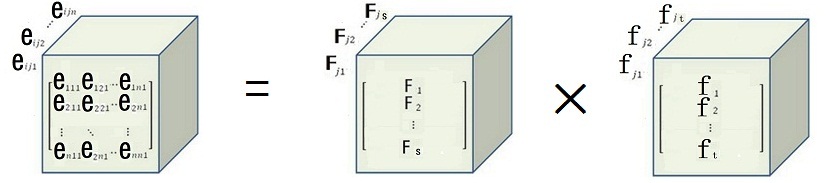 ) _' v5 ]: V" ^& O6 `* c ) _' v5 ]: V" ^& O6 `* c
4 Z! ~( }8 _3 A1 u7 }% G2 d0 Z* z K" d O9 R6 [8 x9 E
s2 w: Z. ~' C2 a% j( W# q" R" N8 V0 L
6 n: y7 R3 j$ j0 S4 E4 {: `# b/ |) G. A/ w. \; t* h. e' J
1 g+ z- j( l" D; }/ v; f9 i
% k7 y+ Y% \6 u. C1 h0 F6 y, U0 o$ i7 A4 H
其中,F为水果的“属性”是空间、f为水果的“种类”是空间、e是“属性×种类关系”的多重线性关系下的张量空间+ `- k7 E( {: c4 C
* V( H; D" \& Q- ], Q$ ^) B
0 y1 O0 g n/ Z; ?2 ?" j6 m5 u
) i- E# _' q6 x" T$ X0 B
7 A- H" ?0 k* |
0 R- d# u1 a+ P. I8 [
0 L& a! C3 G* `5 w, n7 @6 }) Y8 @7 S# W7 ^6 O9 a# A
9 n. `2 ~5 ?9 F4 f
% u% J( y- u0 w; t1 B
7 C, E0 W5 d8 r% b( o$ k
$ r/ i. \! o; S6 s8 _
. v8 b! e" B ]$ G6 X/ ?; J4 }- R3 `( @; K
6 ?! x' \- p' A; E5 r
& b: m$ G0 A+ }- c/ ?' z; Y6 T/ i5 j4 Y T& D0 V
3 d, L4 V' j5 h. r; r2 [# L- v
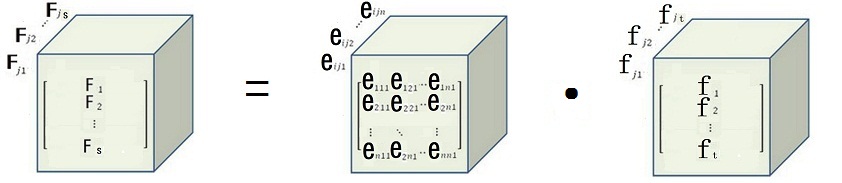
( Z% ]7 I8 b1 V! c/ w+ U0 n 上面的式子还可以表达为:( X, i2 ^8 l% T; M7 I
9 }& r h: {1 i( F- H, s! P$ j& w
6 x# e, O- y: b0 f: F& n: ~
6 J/ E- j% W. M5 I; z; v: X
7 [% p; {7 q# v/ }5 n% r& Y- b |) Q6 s/ m7 R
' g) \# d. T7 {9 J4 ~, B8 r+ Y( h! h$ n% s5 d( S
; Z `! R. T& R9 x0 r
# d+ [) ^9 r* e. l: m2 w- K( B4 y4 H+ l9 t+ @6 ?5 q$ D# m/ K
即:属性= 关系 * 种类7 h* C2 ? p. {$ l
& _+ b8 y( o7 E
. O' z! D$ \ C/ \ 哈哈,有点像我们熟悉的力学关系式 F=ma R* P6 ]0 M& w8 K) N
- K9 D3 Z1 d4 R
$ {. e6 C. V. ?) y: V1 p$ c3 c" s: u" {" x5 Z
" \ Q9 \: @2 G X
7 c, {. q: i; E4 v+ ^8 y; j/ J
+ x1 M) i( y! a U6 C 结合本章第一节的介绍,F、a如果是单属性向量,则关系式 F=ma 说明F、a具备线性关系+ q% Z( f- F, U; j6 P1 G
+ U( I+ o5 l5 w0 O6 [7 E
+ c! x( G; Y* w0 z 但如果F、a是多属性高阶张量,则“点”概念F、a不是线性相关的,而是“系统”概念下的‘多重线性关系’
4 I2 Z6 ?2 [2 i" S- X: M: h: F D; v5 I# _% b6 F% B2 ~
, H4 H% ^+ \0 |( _
5 c& P6 i4 `* s; w& {1 ^& @
a5 K9 W( S# A) B/ V8 F1 D! ~5 G
! W& e2 r t5 C( |
1 k: j9 H( p* b3 Z 同理,高阶张量模型中的一篮子水果的“属性”和“种类”,虽然不是线性相关的,但却具备“系统”概念下的‘多重线性关系’# \, A+ z5 b0 ~
o! [% }/ S/ T5 A/ a
! I6 A8 `$ ~& I- k% Q) P0 k# I; `' H) X( I T8 L0 U
- \1 l( b$ }) k, g/ e) U! _4 t' P, E( b/ _& d
2 Z( m9 Y" u, m! r
: @3 r# p* @2 E
/ [4 ?6 M* U# |" ]/ {* D5 i
3 T/ T9 A' S; k/ H7 d# O
' x& c! G6 @- [
" N$ l. }6 T# @7 o/ g$ g3 u5 u1 E; c$ y5 @) p& L, T | S
( {8 h7 C9 q& E3 w$ O( [/ t/ @9 u
7 ~" A+ h- ]- w: |6 ^" i# @" d 通过张量,我们可以观察推导系统和系统之间的更加精细广泛的关联。并且,利用张量表达式,把一个收敛数据集合的“系统概念”看作一个“点概念”,能够简单表达一个系统和另一个系统的“关系”。原本复杂的多重线性关系,可以简化为某种容易看清的逻辑轨迹,可以明晰其中的规律性。7 H+ ^2 c. v3 I, {, C" S$ r% g
+ P9 _4 @. P0 Q* W& a7 m4 S" [6 [ P- ?( p* V) e" z+ x ]. G, o
因为复杂的对象一般来说我们无法计算,但是局部可以用线性的对象去模拟,这就是阿列夫1维度空间的微积分的基本思想。这个可微分的光滑曲线的局部直线段dx是一个向量,微分dx的全体组成了一个线性空间。1 a) R0 s) E2 U: l
# e6 i& \% E( t; ] Y/ m0 B
~. t6 k# X; B8 s& G6 F. e) Y' Q 进一步,如果多维“属性”都可以依次偏微分,则全体的偏微分的形成了多重线性相关性。这样,我们不只可以研究两个空间之间的一阶线性映射,还可以研究任意多个空间属性分量之间的多重线性映射。, ?( y2 i1 S1 ]# x3 I
, Z: V" l& s* S* W" A& D
* m: t7 u f; Y: R, u- m1 @ W/ }1 g0 g+ v$ b& W+ o! q6 ?% ^2 ^
) e/ }# V% F# j- i5 U2 A3 c- O+ o- l' P# ?/ I( j* N ~ V6 L& L
5 m7 o' z# I. V8 }
( h7 \9 l: T) h4 b
& M6 M: Z. W* B1 n' G6 F1 J4 y. F. V
' L) N% v! ]+ ?9 R& ]
" }7 N. K6 W( ` 比如,如果能够量化亚马逊河鲟鱼等动物和可可树等植物等不同生物种类的各种不同属性(比如氮、磷、钾养分含量)的分量关系,就可以量化研究亚马逊生态圈的养分如何流动:
2 u4 T7 @2 m" w7 L0 I: O! h# [# U. M- N8 W& {) l6 j
9 c! P r% w* u4 H7 A4 ~
( f( X. D' z: n4 ~
7 q: U, ]; _$ g) V s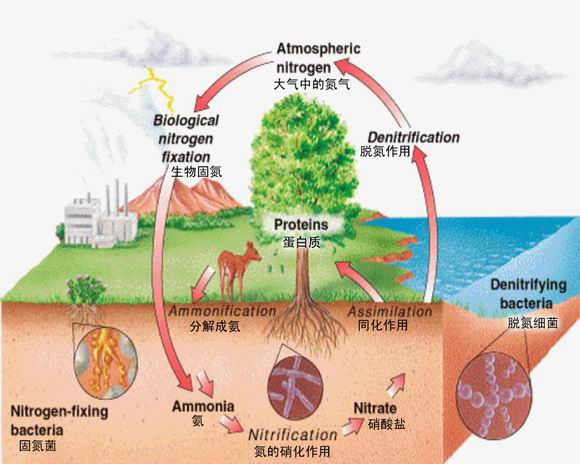 7 i! [/ y5 A. G4 a. j1 S, e* y 7 i! [/ y5 A. G4 a. j1 S, e* y
( a- t/ A+ P% z6 Q1 i5 h
- M; V& j @. ^( P( l6 W
, r$ \0 _. p2 x3 V
A- H! w3 G( v" ^
* [6 i; u1 S; k d$ i- |
2 r1 g& z7 o9 M0 s) h& }: n5 e* T
/ w& M9 Z9 \4 R, |5 m& i$ Y' |+ `+ P6 m/ o$ y- O1 d g0 F
5 E/ ^7 F `/ j
. B0 S* R: Q9 k. Y* i' ?( |+ C- j- V' r4 ^0 D
: }" `# t2 ~4 s/ a
又比如,通过偏微分分量(泊松括号)可以表示哥本哈根矩阵力学的运动轨迹:
* [$ F6 `; R: x! _8 o" k* ^+ k% O
4 E( z& c8 g; e3 g/ L" X. Z5 @& F+ d+ D/ _- R! X: F6 j
- J0 L" v Y% v' V- ^7 \1 u5 H4 L+ _) [
 n3 D. [( U/ P' v. F; M n3 D. [( U/ P' v. F; M
0 Y4 |/ A9 Z; ]/ r( r1 s4 ]8 Y* Z+ R% [9 h& ^8 k
2 `) v! D# u* |6 R5 H& H
/ ]' p: k( C9 e4 Z8 q8 L
) u7 N! q' c5 b8 D6 S9 |5 Y" M, G/ g$ ]+ H. Y
- Q9 n- @8 ?) `. x& R) h6 O* q, W" T; y, n8 f4 ]8 u( T( C9 j1 E
r" E6 D5 Q7 Z) A5 A5 z. J
4 }; v2 K# w. \" ]9 u' A
# L k7 T. ?/ l" s: a
+ o8 p* }0 Y+ a0 K4 z$ @
" G9 S) }& s8 W: T" l/ z 动量×坐标矩阵(二阶张量)傅立叶变换的形式如下:
% z9 Y# j4 S7 n! G0 J4 y) ]# R; J# P; [
7 f% @4 m0 L" U% i, I
2 v7 T7 y' z9 t: O" [
6 B; h! r2 F8 h* A" o7 q
' V1 A3 y6 C' i
( P7 {# ~+ a; f R3 d/ j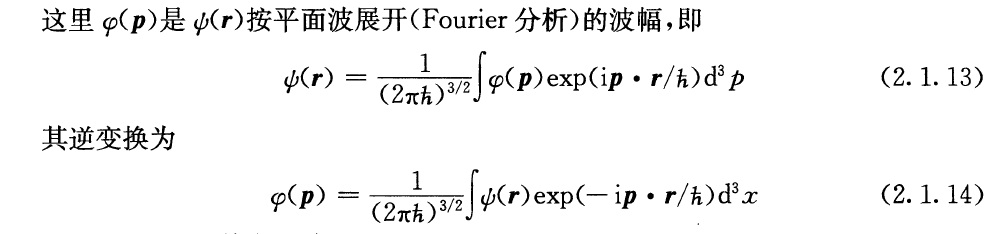
* Q* L3 X5 ?6 @0 V; M- f4 R( x9 _: v! d! r
" a+ b: D- J4 e2 P8 u) z5 J) ~
; \7 G: `) k; J" u
+ d3 i! Z' D% K: R/ y
# k0 R6 A6 V; }- Z, E2 a' s- j& j1 ]2 e# Q
0 `$ f% l ]5 F 高阶的量子态张量空间(高维度傅立叶变换)可以表示如下:
" w6 v8 P( u; q' d
5 Z |1 k" E& D. `& L
# y: i% Q4 W( }: z " O( [6 o _# H+ { " O( [6 o _# H+ {
6 U6 Q$ Y2 j$ K% V, |; n
0 @2 N5 N: ]# k1 y2 e+ E4 z* o
% f) `5 w9 N1 n Q) l9 E
% t, N: s/ X$ u" ^
) {1 o* m! f! l/ g$ Q1 h+ _6 a0 s N# p2 P% r) U
- J9 I# Z- ^6 a# x 注意,上面这个式子就是未来量子计算机的基本演算模型,它的子式子可以是∞ ^∞ (无穷大的无穷大次方)。其异常复杂的程度,超过想象! f E+ I% N" E5 z. E' L6 c" p
0 m9 J; M% l, b
7 g# M# D9 s, U4 o7 L; u* H4 P- ^# k
$ }" N, p9 s5 W; _. A$ e
, n2 \) n0 a! h$ {0 h$ {% D6 w' W! k" O' B1 J5 k$ ~
4 l8 u/ V+ u+ v9 R. x/ r' k. p2 K1 X% O( [8 S, V
" ^; f, K$ C, f* b9 y" {
- p. G, }" F' s% [8 |9 U
4 K) t+ E( i) U0 X" L7 {0 g
) @- O6 X9 e) L' B. M0 v5 `
- A9 X5 s" g; C- S" ?4 H& v& V" ?5 U* G! K6 S) ~
. G5 C- B( Z/ d3 z
1 e) ^, f0 u5 [) S" B) s
. [! r7 J2 j$ \8 q8 E6 M
( a( h2 F! X; Y: \5 k% `& @' E
; {* R- k7 T0 R1 X5 c) h
$ l# O4 I+ `7 q) S. h; J" p' H
" ^; v' H8 o7 @, |( D0 g5 E/ Q/ _3 ~' v& E
+ S! Z) y# d U( b! D3 o: C4 k
0 ~1 ?; W; E6 z: n* j/ O7 M, T& W" E! K0 u
+ L. E6 r+ M( U' B! x- H: {
2 h, B3 [% U1 x G3 F
5 ]% D3 x; y" x9 o& r( n, ^$ ^
- [! X p. q6 h% C
! g0 `" B* t R1 T% V 高阶张量的计算如何超乎想象的,我们简单来看看。下面是动量×坐标的傅立叶变换矩阵:6 m! Z) l. p# c0 H! v$ R# J
2 q- l( R$ I4 r, K1 Q1 ]7 u) P# t i( ^
; |; s8 g7 `, j( E5 c1 H2 U1 V
0 f& P+ B& M! b/ L9 y4 v3 A
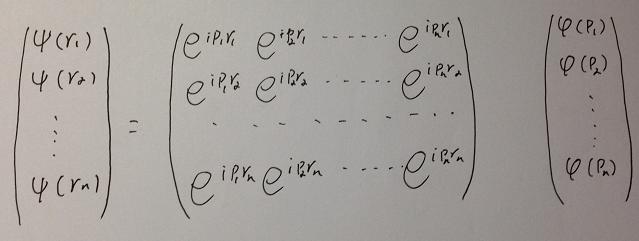 - L* j' M, H; o3 h7 X* J - L* j' M, H; o3 h7 X* J
3 \- Y$ @: U5 N( ?
因为exp(ipr)可以作为所有线性时不变系统的基,所以也可以把exp(ipr)作为系统的基矢量。当我们把exp(ipr)看作基矢量,则是另一种矩阵形式 φ . exp =Ψ,如下图:( G- v2 [) @, H \$ b, j
7 F6 J" B# f5 P" j! u& n/ \6 |: x- }
 2 V/ { t: ?7 ? 2 V/ { t: ?7 ?
3 x" ?4 q4 \- U+ }! @4 B* Q& F7 t3 F6 \2 |
+ q/ M; g9 C+ G4 f; R1 n+ L5 j( }& X 当前,我们使用的基于经典物理模式的电子计算机就是按照这种串联方式演算的。以线性字符串演算高阶张量,乍看起来似乎可以,其实不然。因为数据量异常庞大,比如上面的φ矩阵其实已经扩展到了 n平方*n平方维度
: x3 Y6 f8 j8 ?) j9 |( o/ L" u' P# u4 \1 F
: s6 h/ }+ k- }, w
并且,由于高阶张量不仅仅限于平面矩阵,如下图,我们还可扩展到三阶张量:
; n3 M2 \* N6 q4 N/ \+ S( N- p/ x8 ~
* g# J: L! T1 l. p/ {) n
+ J! |9 b7 [1 \( U
0 {% B' }3 `9 i# \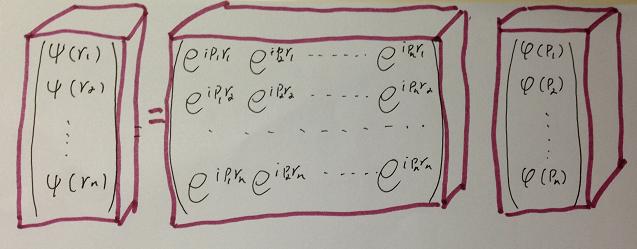
' M( s7 A9 X* }1 x
; Z7 J6 E9 \9 W* I6 o& c. s 我们知道,高端服务器所依赖的unix操作系统具有多进程并行处理能力,但那其实只是分享时间片段的伪逻辑并行,有不可避免的局限性,因为电子计算机的物理模型仍然是经典物理的字符串。在三阶、四阶......n阶张量的情况下,数据量将突破连续实数所能表达的范围(阿列夫1),即使在理论上,字符串运算的电子计算机也根本无能为力。3 k. E+ e* E6 k, ~' p
2 \4 m3 x7 }1 U+ L' ^
- e. B/ {- g: }5 I# Q8 z: L$ Z2 k% S- f+ T+ a
5 O j; W% d- p% o# h7 h5 L
+ J4 D) |% F$ s* C9 a. ^
! k7 P; Z; Q$ `% a B
" ~9 F! z- t- d8 J" A$ }
; C" \( _" h/ A% x. M9 I6 H' Q! a1 F9 @" H, S' ^4 W! f
7 f X6 ?: T0 _1 c2 K
. ?. B x, A" b: p6 U
2 I& z5 R- S$ C
7 m* _( \2 e+ R
, U& v- a5 Q4 q4 G
4 o9 E' E" c4 i, W" f8 O) d. S" l; Z2 m' f1 G$ K- L
: T" }% W D, E- e3 U: a6 |+ H& O( ~8 T7 B& I; M
但是,基于量子叠加原理的量子计算机,却可能拥有2^n (2的n次方)的并行计算能力。这是质的飞跃,因为当n等于250时,量子计算机可同时并行处理比全宇宙所有原子数目还多的数据。
3 h& z9 r. h5 n* d d3 v) D1 _ V
" C/ J6 o& ?, T- a
5 c$ I% o: s3 F9 D
# l6 c2 `2 y8 A v
# u5 i$ h9 G( I# C( ~- x+ Y4 C
* H6 x8 W" l; N9 M- a6 L* [+ E4 t, j- a+ Y8 }0 ?& d
$ g, h0 P+ d( ~% `3 m+ s. [8 ^- o& H
: {& Z- H( C" Y. R6 s8 r5 y
0 n: O. a$ A G1 {; `
S8 C; L+ X- Y0 R5 W/ R+ @: \
/ ` {8 b: C! f* \8 `! m# ]$ ?. L2 ^4 |) m7 S
' I8 `' D* W9 t, G, f% j
% q9 x" h; A* F" c$ E6 i/ c
2 z p& W2 [% p) S. R
; s+ R# r9 P7 ~: ^* V2 H4 B* D' Y/ O* y6 T, K0 @ x
关于"大数",最早表述在古希腊数学家阿基米德开始,他在理论上提出了一种表示大数的方法:有人认为,无论是在叙拉古城,还是在整个西西里岛或者在世界上有人烟和没有人迹的地方,沙粒的数目都是无穷的;也有人认为沙粒的数目不是无穷的‘但是想表示沙子的数目是办不到的……但是,我要告诉大家,用我找到的方法,不但能表示出占地球那么大地方的沙粒的数目,甚至还能表示把所有的海洋和洞穴都填满了沙粒,这些沙粒总数不会超过1后面有100个零。
* ?; v9 J5 ^7 K
! b& l5 Q& a' h. K1 _$ T5 R2 B% ~; C3 Z0 b* @1 T j" u
在这段文字中,“1后面连续有100个零”即10^100(10的100次方),按数位念作“一万亿亿亿亿亿亿亿亿亿亿亿亿”
# e% I0 E/ `, i' Y+ S! K" a% n8 {* W6 b( D. P* K7 ~
/ r' p$ ?- ]+ @1 M+ j1 u3 i' z4 p9 D) b0 l& h: r
+ s2 k$ ]; `7 `# E' m4 `/ C% I
0 r4 i. \( m* I$ G! S6 ^- D' S8 d7 x: `. t% Y
10的100次方已然如此恐怖,那么下面这个东东呢?! C( ?9 Q' m( {3 N% C+ x( H4 b
' K4 ^* p: F( \4 S6 \8 y, u+ B+ B% t3 v
) p. e' X3 ]5 c+ R; v3 u6 k5 b, Y4 G
& q8 j* f0 v, f# P; Q# e" h8 ^7 ]" c) Y

6 Y0 H; @2 ^" W, p6 D, @
0 j G9 ?2 D8 j' [. {
2 A# G: n' p! i* ^+ ^5 r) l' | N
! K7 O& H- K5 R) F6 d
2 R V, A. m( N' \# H2 Q5 L) G4 s% ^5 {6 L) X5 ^: I1 G+ A6 L V+ m
; }9 B: d5 v# M* i$ c/ b! E& S
1 J; ? D' a) a6 l" M7 k3 x& Z4 E+ w- ~) H8 F
. u, T! _& q& V4 n' Q
! V5 g" B9 [ b- A3 v' T$ x: R" n$ f
5 o; w& H! Q: R1 p# x/ {" t# u& ] ]8 K& G$ [
* Q& @: @$ ?7 @: P& l
+ [/ Y; z. [7 r+ j8 ?9 ^- x4 T: l* n& N, v5 B' R! N
0 `: {5 s$ }( z( x
8 [( O% q' M$ M0 Z6 W0 Q6 p1 @7 w; I: N( y
. R" {1 q$ I/ [$ A' @
7 y1 g; H/ b) c3 ?) T" `5 q7 {' T
% X6 J4 S4 m; o5 W; ^7 [
; R- m A- S) ]7 A- O$ K P& ` h- q w9 l3 \; C# H3 A3 O
4 } i% |9 ?: P* j7 k
& x6 \1 W* x* P* @4 \0 K* V
4 Q6 I# K, G: F5 k: h- Q$ n8 k e5 O+ d- }
5 u3 K V6 n t2 j5 c1 ^
# y" h$ F. X/ F0 e7 q& S1 }+ K% U* q4 Q6 c. M- l# a
" G" O, h2 W+ i$ U8 l$ m2 w$ K! U2 r* p# o* }5 W1 j7 K4 ~+ V( m
3 R, o8 s* F, g+ R! w2 k
. `0 x* ?7 N& f1 k, B/ l
% A" t- I4 d+ \' w9 ^) n1 `
[4 ?0 h" t/ C1 G3 o8 u% c3 o* N; |7 h, M& D6 A8 w, i9 A
) N7 ^ X a" P9 f4 |$ Z& T% P3 i
9 ?/ {- w, h# S, M5 k: w ?; S3 b/ e6 G6 u" m( W
: N$ f5 d+ M, D& B5 V( w6 D- w" N9 `) D
4 t3 q. b% H0 A4 {; w/ t' @' D
; [7 L: _# {. g" U# V
- G, |8 g6 F$ m4 }$ E6 i
9 x9 y) k1 ]- d5 m. s7 o5 f! Q( p7 ~" F
5 }- H8 f3 c/ V3 A+ }; [* a1 [
还有,更多的,更多更多更多的:4 ^8 q% e* |9 m: i' `' J: i& j
1 ?5 T. I* I8 x; Z# Y1 E4 m0 ?
: p _* p1 A8 @% [2 U! e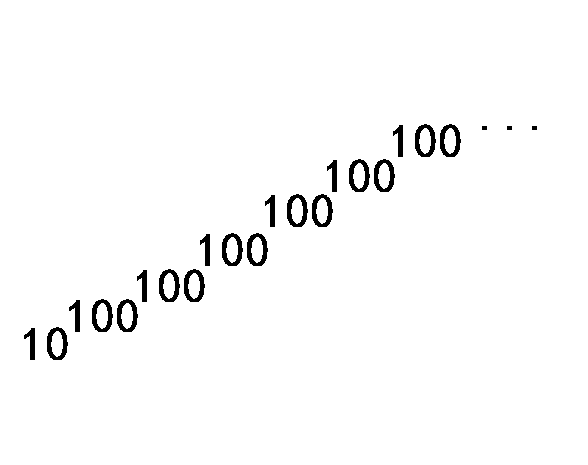 . ?5 q& ]0 i8 w6 O4 m . ?5 q& ]0 i8 w6 O4 m
- a3 s! Q* X5 j/ n' ?; G/ O
& E# g8 \5 p7 }. ?6 V$ ]# P% x/ S) ^6 Y6 O6 P
这是张量允许的。
' s6 N6 L* {/ y$ V$ o3 C, }# y' o
|
|